题目内容
3.已知数列{an}为等比数列,则下列结论正确的是( )| A. | a1+a3≥2a2 | B. | 若a3>a1,则a4>a2 | C. | 若a1=a3,则a1=a2 | D. | a12+a32≥2a22 |
分析 根据等比数列的通项公式、不等式的性质进行解答.
解答 解:设{an}的公比为q.
A、因为a1+a3=a1(1+q2),a3=a1q2,所以当a1<0时,该不等式不成立,故本选项错误;
B、若a3>a1,即a1q2>a1.a4=a1q2•q,a2=a1q,由于无法判定q的正负,所以无法比较a1q2•q与a1q的大小,故本选项错误;
C、若a3=a1,即a1q2=a1,则q=±1.当q=-1时,等式a1=a2不成立,故本选项错误;
D、因为a12+a32≥2a1•a3=2a22,故本选项正确.
故选:D.
点评 本题考查等比数列的通项公式及应用,考查计算能力,属于基础题和易错题.

练习册系列答案
相关题目
14.在△ABC中,若a=$\sqrt{3}$,b=$\sqrt{2}$,b=45°,则∠A的为( )
| A. | 30°或120° | B. | 60°或120° | C. | 30° | D. | 60° |
18.已知幂函数f(x)=xn的图象过点(8,$\frac{1}{4}$),且f(a+1)<f(2),则a的范围是( )
| A. | -3<a<1 | B. | a<-3或a>1 | C. | a<1 | D. | a>1 |
8.执行如图的程序框图,输出的S的值为( )
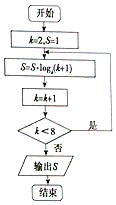

| A. | 6 | B. | 5 | C. | 4 | D. | 3 |