题目内容
数列 满足
满足
(1)证明:数列 是等差数列; (2)求数列
是等差数列; (2)求数列 的通项公式
的通项公式 ;
;
(3)设 ,求数列
,求数列 的前
的前 项和
项和 。
。
 满足
满足
(1)证明:数列
 是等差数列; (2)求数列
是等差数列; (2)求数列 的通项公式
的通项公式 ;
;(3)设
 ,求数列
,求数列 的前
的前 项和
项和 。
。(1)见解析(2)  (3)
(3) 
 (3)
(3) 
试题分析:(1)取倒数得:
 ,两边同乘以
,两边同乘以 得:
得:  所以数列
所以数列 是以
是以 为首项,以1为公差的等差数列.
为首项,以1为公差的等差数列.(2)
 即
即
(3) 由题意知:
 利用错位相减得:
利用错位相减得: 
 利用错位相减得:
利用错位相减得:  ,
,
点评:错位相减法数列求和是学生不易掌握的地方

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足
满足 (
(
 ,2,…,
,2,…, ),若
),若 ,
, ,则
,则 =
=  中a3+a4+a5=12,
中a3+a4+a5=12,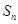 为数列
为数列 项和,则S7=( )
项和,则S7=( )


 的通项公式
的通项公式 ;
; 求数列
求数列
 证明:
证明: 。
。 中,
中, ,
, ,则
,则 等于( )
等于( )



 是等比数列
是等比数列 的前
的前 项和,且
项和,且 .
. ;
; 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围. 中,
中, 的值是( )
的值是( )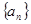 的前
的前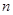 项和为
项和为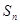 ,且满足
,且满足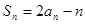 ,
,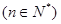 .
.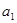 ,
,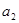 的值;
的值;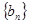 的前
的前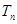 ,且满足
,且满足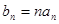
 中,
中, ,则
,则 的值是( )
的值是( )