题目内容
已知:数列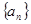 的前
的前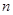 项和为
项和为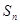 ,且满足
,且满足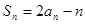 ,
,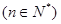 .
.
(Ⅰ)求: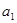 ,
,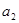 的值;
的值;
(Ⅱ)求:数列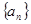 的通项公式;
的通项公式;
(Ⅲ)若数列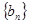 的前
的前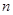 项和为
项和为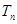 ,且满足
,且满足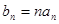
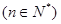 ,求数列
,求数列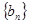 的
的
前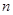 项和
项和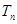 .
.
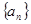 的前
的前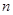 项和为
项和为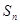 ,且满足
,且满足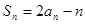 ,
,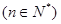 .
.(Ⅰ)求:
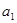 ,
,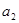 的值;
的值;(Ⅱ)求:数列
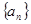 的通项公式;
的通项公式;(Ⅲ)若数列
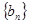 的前
的前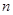 项和为
项和为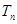 ,且满足
,且满足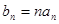
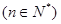 ,求数列
,求数列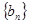 的
的前
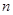 项和
项和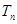 .
.(Ⅰ)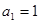 ,
, (Ⅱ)
(Ⅱ)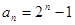 (Ⅲ)
(Ⅲ)
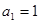 ,
, (Ⅱ)
(Ⅱ)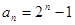 (Ⅲ)
(Ⅲ)
试题分析:(Ⅰ)因为
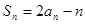 ,
,令
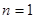 ,解得
,解得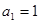 ;令
;令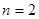 ,解得
,解得 , ……2分
, ……2分(Ⅱ)
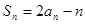 ,
,所以
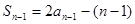 ,(
,(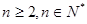 )
)两式相减得
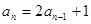 , ……4分
, ……4分所以
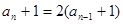 ,(
,(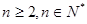 ) ……5分
) ……5分又因为
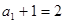
所以数列
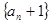 是首项为
是首项为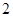 ,公比为
,公比为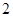 的等比数列, ……6分
的等比数列, ……6分所以
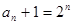 ,即通项公式
,即通项公式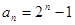 (
(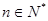 ). ……7分
). ……7分(Ⅲ)
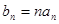 ,所以
,所以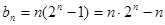
所以
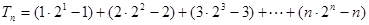
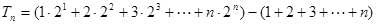 ……9分
……9分 令
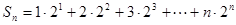 ①
① ②
②①-②得

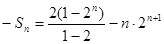 ……11分
……11分 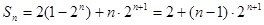 ……12分
……12分所以
 . ……13分
. ……13分点评:数列的递推关系式也是给出数列的一种常见形式,由递推公式求通项公式的方法有累加、累乘和构造新数列等,而求和需要掌握公式法、分组法、裂项法和错位相减法等方法.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 满足
满足
 是等差数列; (2)求数列
是等差数列; (2)求数列 ;
; ,求数列
,求数列 的前
的前 项和
项和 。
。 中,已知
中,已知 .
. 求数列
求数列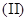 设数列
设数列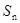 ,求
,求
 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, ,
, ,数列
,数列 为等比数列,求实数
为等比数列,求实数 的值;
的值; ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前n项和
的前n项和 .
.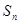 是等差数列
是等差数列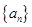
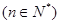 的前
的前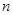 项和,且
项和,且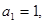
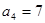 ,则
,则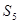 =
=  中,
中, ,则
,则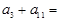 ( ).
( ).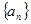 的前
的前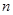 项和
项和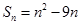 ,第
,第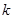 项满足
项满足 ,则
,则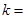
 中,已知
中,已知 ,那么
,那么 =
=
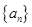 的前
的前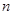 项和为
项和为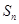 ,且满足
,且满足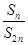 为常数,则称该数列为
为常数,则称该数列为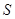 数列.
数列.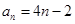 是否为
是否为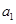 且公差不为零的等差数列
且公差不为零的等差数列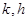 满足
满足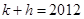 ,求
,求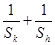 的最小值
的最小值