题目内容
16．已知圆C：（x-3）2+（y-2）2=5，一束入射光线从点A（-1，1）出发经直线x+y+2=0反射后与圆C相交于点P，求入射光线从点A到点P的最短路程为（ ）| A． | $\sqrt{5}$ | B． | $2\sqrt{5}$ | C． | $3\sqrt{5}$ | D． | $4\sqrt{5}$ |
分析 先求点A（-1，1）关于直线l：x+y+2=0的对称点为A′，连接A′C与圆交于B点，则AB为最短的路线，利用两点间的距离公式求出A′C，然后减去半径即可求出．
解答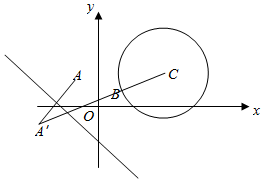 
解：设点A（-1，1）关于直线l：x+y+2=0的对称点为A′（a，b），
$\frac{b-1}{a+1}=1$，$\frac{a-1}{2}+\frac{b+1}{2}+2=0$，解得a=-3，b=-1，即A′（-3，-1），
由反射原理可知，A′（-3，-1）在反射光线上，
当反射光线过圆心C时，
光线从点A经反射到圆周C的路程最短，最短为|A′C|-R=$\sqrt{（-3-3）^{2}+（-1-2）^{2}}$-$\sqrt{5}$=2$\sqrt{5}$．
故选：B
点评 本题考查了圆的标准方程，考查了直线和圆的位置关系，考查了数形结合的解题思想方法与数学转化思想方法，是中档题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
10．在△ABC中，角A、B、C的对边分别为a、b、c，且$\frac{2a}{bsinA}$=3，则sin（π+B）等于（ ）
| A． | $\frac{3}{4}$ | B． | -$\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |
11．在△ABC中，A=$\frac{π}{6}$，AB=2，AC=3，点M在BC上且满足$\overrightarrow{CM}$=2$\overrightarrow{MB}$，则$\overrightarrow{AM}$$•\overrightarrow{BC}$=（ ）
| A． | $\frac{1}{3}$+$\sqrt{3}$ | B． | $\frac{1}{3}$-$\sqrt{3}$ | C． | $\frac{11}{3}$+$\sqrt{3}$ | D． | $\frac{11}{3}$-$\sqrt{3}$ |
5．
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（0）+f（$\frac{11π}{12}$）的值为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（0）+f（$\frac{11π}{12}$）的值为（ ）| A． | 2$-\sqrt{3}$ | B． | $-2-\sqrt{3}$ | C． | 1$-\frac{\sqrt{3}}{2}$ | D． | $-1-\frac{\sqrt{3}}{2}$ |