Question

【题目】已知直线l：4x+3y+10=0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方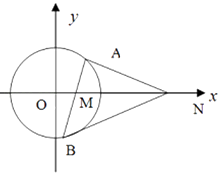

（1）求圆C的方程；
（2）过点M（1，0）的直线与圆C交于A，B两点（A在x轴上方），问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：设圆心C（a，0）（a＞﹣ ），

∵直线l：4x+3y+10=0，半径为2的圆C与l相切，

∴d=r，即 =2，

解得：a=0或a=﹣5（舍去），

则圆C方程为x2+y2=4；

（2）解：当直线AB⊥x轴，则x轴平分∠ANB，

若x轴平分∠ANB，则kAN=﹣kBN，即 + =0，

整理得：2x1x2﹣（t+1）（x1+x2）+2t=0，即 +2t=0，

解得：t=4，

当点N（4，0），能使得∠ANM=∠BNM总成立．

【解析】1、根据直线与圆相切d=r可求得a=0即得结果。
2、由题意当直线AB⊥x轴，则x轴平分∠ANB，即得kAN=﹣kBN，可求出关于x的一元二次方程，利用根与系数的关系表示出两根之和与两根之积代入上式可得到t=4，即得点N（4，0）。