题目内容
2.命题“?x∈R,3x>2x”的否定是( )| A. | ?x∈R,3x≤2x | B. | ?x∉R,3x<2x | C. | ?x0∈R,3x0≤2x0 | D. | ?x0∉R,3x0<2x0 |
分析 利用全称命题的否定是特称命题写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题“?x∈R,3x>2x”的否定是:?x0∈R,3x0≤2x0.
故选:C.
点评 本题考查命题的否定,全称命题与特称命题的否定关系,是基础题.

练习册系列答案
相关题目
12.已知$f(x)=\left\{\begin{array}{l}a-{x^2}-2x,x≤0\\{e^{|x-1|}},x>0\end{array}\right.$,且函数y=f(x)-1恰有3个不同的零点,则实数a的取值范围是( )
| A. | (-1,+∞) | B. | (-2,0) | C. | (-2,+∞) | D. | (0,1] |
14.已知数列{an}满足a1=1,a2n=n-an,a2n+1=an+1(n∈N*),则a1+a2+a3+…+a40等于( )
| A. | 222 | B. | 223 | C. | 224 | D. | 225 |
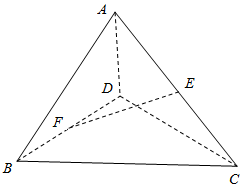 空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.
空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.