题目内容
点A是函数f(x)=x3+4x+5的图象在x=1处的切线上的点,则点A到圆2x2+2y2-8x-8y+15=0的最短距离为( )
分析:求出函数在x=1处的导数,就是这点处切线的斜率,求出切线方程,将圆心代入点到直线距离公式,求出圆心到直线的距离,减去半径可得答案.
解答:解:因为函数f(x)=x3+4x+5,所以f′(x)=3x2+4,
所以函数f(x)=x3+4x+5的图象在x=1处的切线的斜率为:k=7,切点坐标为(1,10)
所以切线方程为:y-10=7(x-1),即7x-y+3=0,
圆2x2+2y2-8x-8y+15=0的圆心(2,2)到直线的距离d=
=
大于圆的半径
,
所以直线与圆相离,
则点A到圆2x2+2y2-8x-8y+15=0的最短距离为
-
=
故选C.
所以函数f(x)=x3+4x+5的图象在x=1处的切线的斜率为:k=7,切点坐标为(1,10)
所以切线方程为:y-10=7(x-1),即7x-y+3=0,
圆2x2+2y2-8x-8y+15=0的圆心(2,2)到直线的距离d=
| |2×7-2+3| | ||
|
3
| ||
| 2 |
| ||
| 2 |
所以直线与圆相离,
则点A到圆2x2+2y2-8x-8y+15=0的最短距离为
3
| ||
| 2 |
| ||
| 2 |
| 2 |
故选C.
点评:本题是中档题,考查利用导数研究曲线上某点的切线方程,直线与圆的位置关系,考查计算能力.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
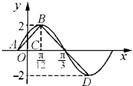 函数f(x)=2sin(ωx+φ)(其中ω>0,
函数f(x)=2sin(ωx+φ)(其中ω>0,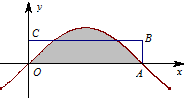 (2012•湖北模拟)点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于
(2012•湖北模拟)点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于 点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示).若图中阴影部分的面积等于矩形的面积,那么边AB的长等于
点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示).若图中阴影部分的面积等于矩形的面积,那么边AB的长等于 函数f(x)=2sin(ωx+φ)(其中ω>0,
函数f(x)=2sin(ωx+φ)(其中ω>0,