题目内容

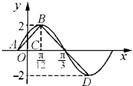精英家教网函数f（x）=2sin（ωx+φ）（其中ω＞0，-
π
2
＜φ＜
π
2
）的图象如图所示，若点A是函数f（x）的图象与x轴的交点，点B、D分别是函数f（x）的图象的最高点和最低点，点C(
π
12
，0)是点B在x轴上的射影，则
AB
•
BD
的值是（　　）
A、8
B、-8
C、
π2
8
-8
D、-
π2
8
+8
分析：结合图象先求函数的周期，求出ω，推出φ，然后求出
AB
，
BD
；再求
AB
•
BD
即可．
解答：解：由图可知
T
4
=
π
3
-
π
12
=
π
4
?T=π，
∴ω=2，
又2•
π
3
+φ=π?φ=
π
3
，
从而A(-
π
6
，0)，B(
π
12
，2)，D(
7π
12
，-2)，
AB
=(
π
4
，2)，
BD
=(
π
2
，-4)，
AB
•
BD
=
π2
8
-8
故选C．
点评：本题考查三角函数的周期性及其求法，平面向量数量积的运算，y=Asin（ωx+φ）中参数的物理意义，考查学生分析问题解决问题的能力，是基础题．
练习册系列答案
相关题目
已知函数f（x）=2sinωx（ω＞0）在区间[-
π
3
，
π
4
]上的最小值是-2，则ω的最小值是
 
．
若函数f（x）=2sinωx（ω＞0）在[-
2π
3
，
2π
3
]上单调递增，则ω的最大值为
 
．
（2013•盐城三模）已知函数f （x）=2sin（ωx+?）（ω＞0）的部分图象如图所示，则ω=
2
3
2
3
．
已知函数f（x）=2sinωxcosωx-2
3
sin2ωx+
3
（ω＞0），直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1-x2|的最小值为
π
2
．
（I）求ω的值；
（II）求函数f（x）的单调增区间；
（III）若f（a）=
2
3
，求sin（
5
6
π-4a）的值．
设函数f（x）=2sin（x-
π
3
）cosx．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）讨论f（x）在[0，
π
2
]的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网