题目内容
点A是函数f（x）=sinx的图象与x轴的一个交点（如图所示）．若图中阴影部分的面积等于矩形的面积，那么边AB的长等于| 2 |
| π |
| 2 |
| π |
分析：先利用定积分的几何意义和微积分基本定理，将阴影面积转化为求定积分的值，再利用矩形面积公式等于阴影面积列方程即可解得AB长
解答：解：依题意，图中阴影部分面积S=
sinx dx=（-cosx）
=（-cosπ）-（-cos0）=2
设矩形边AB=x，
则矩形面积为π×x=2
解得x=
故答案为
| ∫ | π 0 |
| | | π 0 |
设矩形边AB=x，
则矩形面积为π×x=2
解得x=
| 2 |
| π |
故答案为
| 2 |
| π |
点评：本题考查了利用定积分的几何意义和微积分基本定理求曲边梯形的面积的方法
练习册系列答案
阅读快车系列答案
相关题目
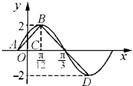函数f（x）=2sin（ωx+φ）（其中ω＞0，
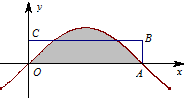（2012•湖北模拟）点A是函数f（x）=sinx的图象与x轴的一个交点（如图所示），若图中阴影部分的面积等于矩形OABC的面积，那么边AB的长等于
函数f（x）=2sin（ωx+φ）（其中ω＞0，