题目内容
在△ABC中设角A，B，C所对的边长分别为a，b，c，且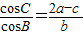
，则角B=（ ）A．30°
B．60°
C．90°
D．120°
【答案】分析：根据余弦定理可得：
，又因为
，所以整理可得2a（a2+c2-b2-ac）=0，即可得到a2+c2-b2-ab=0，再根据余弦定理可得B的大小．
解答：解：根据余弦定理可得：
cosC=
，cosB=
，
所以
，
又因为
，
所以整理可得：2a（a2+c2-b2-ac）=0，
因为a＞0，所以a2+c2-b2-ab=0，
所以由余弦定理可得cosB=
=
，
所以B=60°．
故选B．
点评：解决此类问题的关键是熟练掌握余弦定理，并且加以正确的运算．
，又因为，所以整理可得2a（a2+c2-b2-ac）=0，即可得到a2+c2-b2-ab=0，再根据余弦定理可得B的大小．解答：解：根据余弦定理可得：
cosC=
，cosB=，所以
，又因为
，所以整理可得：2a（a2+c2-b2-ac）=0，
因为a＞0，所以a2+c2-b2-ab=0，
所以由余弦定理可得cosB=
=，所以B=60°．
故选B．
点评：解决此类问题的关键是熟练掌握余弦定理，并且加以正确的运算．
练习册系列答案
相关题目
在△ABC中设角A，B，C所对的边长分别为a，b，c，且
=
，则角B=（ ）
| cosC |
| cosB |
| 2a-c |
| b |
| A、30° | B、60° |
| C、90° | D、120° |
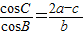，则角B=（ ）