题目内容
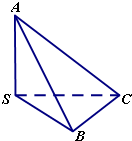 如图,棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为
如图,棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为| 2 |
| 2 |
分析:取BC的中点,连接SD,AD.利用线面垂直的判定定理和三垂线定理可得∠SDA是二面角A-BC-S的平面角.在Rt△SAD中,利用边角关系求出即可.
解答:解:如图所示, 不妨设SA=
不妨设SA=
.
则SB=SC=SA=
.
∵SC⊥SB,BC=
=2.
取BC的中点,连接SD,AD.则SD=
BC=1,SD⊥BC.
∵SA⊥SB,SA⊥SC,SB∩SC=S.
∴SA⊥平面SBC.
∴BC⊥SD.
∴∠SDA是二面角A-BC-S的平面角.
在Rt△SAD中,tan∠SAD=
=
.
故答案为
.
 不妨设SA=
不妨设SA=| 2 |
则SB=SC=SA=
| 2 |
∵SC⊥SB,BC=
| SC2+SB2 |
取BC的中点,连接SD,AD.则SD=
| 1 |
| 2 |
∵SA⊥SB,SA⊥SC,SB∩SC=S.
∴SA⊥平面SBC.
∴BC⊥SD.
∴∠SDA是二面角A-BC-S的平面角.
在Rt△SAD中,tan∠SAD=
| AS |
| SD |
| 2 |
故答案为
| 2 |
点评:熟练掌握线面垂直的判定定理和三垂线定理、二面角的平面角的作法是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中, 如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为
如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为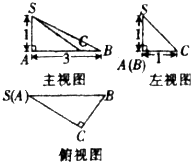 已知三棱锥S-ABC的三视图如图所示,在原三棱锥中给出下列命题:
已知三棱锥S-ABC的三视图如图所示,在原三棱锥中给出下列命题: