题目内容
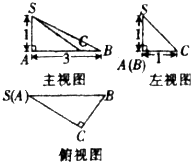 已知三棱锥S-ABC的三视图如图所示,在原三棱锥中给出下列命题:
已知三棱锥S-ABC的三视图如图所示,在原三棱锥中给出下列命题:①BC⊥平面SAC;
②平面SBC⊥平面SAB;
③平面SBC⊥平面SAC;
④三棱锥S-ABC的体积为
| 1 |
| 2 |
其中所有正确命题的个数为( )
分析:根据题意画出图形,①由线面垂直的判定定理即可推出BC⊥平面SAC;
②显然错误;
③由①及面面垂直的判定定理可推出平面SBC⊥平面SAC;
④由三棱锥的体积公式,代入数据即可得到三棱锥S-ABC的体积.
②显然错误;
③由①及面面垂直的判定定理可推出平面SBC⊥平面SAC;
④由三棱锥的体积公式,代入数据即可得到三棱锥S-ABC的体积.
解答:解:由几何体的三视图可知,在三棱锥S-ABC中,SA⊥面ABC,AC⊥BC,且SA=1,AB=3,C到AB的距离为1,如下图示
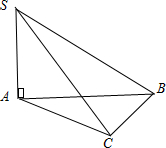
①∵SA⊥面ABC,BC?面ABC,∴SA⊥BC
又∵BC⊥AC,SA∩AC=A,∴BC⊥平面SAC;
②显然错误;
③由①可知BC⊥平面SAC,BC?平面SBC,∴平面SBC⊥平面SAC;
④由题意知,三棱锥S-ABC的体积为V=
×SA×S△ABC=
×1×
×3×1=
.
故答案为 B.

①∵SA⊥面ABC,BC?面ABC,∴SA⊥BC
又∵BC⊥AC,SA∩AC=A,∴BC⊥平面SAC;
②显然错误;
③由①可知BC⊥平面SAC,BC?平面SBC,∴平面SBC⊥平面SAC;
④由题意知,三棱锥S-ABC的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为 B.
点评:本题考查棱锥的结构特征,考查学生发现问题解决问题的能力,射影定理的应用等,是中档题.

练习册系列答案
相关题目