题目内容
 如图,在三棱锥S-ABC中,SA=AB=BC=AC=
如图,在三棱锥S-ABC中,SA=AB=BC=AC=| 2 |
| 2 |
(1)求证:SO⊥平面ABC
(2)在线段AB上是否存在一点E,使二面角B-SC-E的平面角的余弦值为
| ||
| 5 |
分析:(1)利用勾股定理的逆定理、等腰三角形的性质、线面垂直的判定定理即可证明;
(2)通过建立空间直角坐标系,利用两平面的法向量的夹角公式即可得出.
(2)通过建立空间直角坐标系,利用两平面的法向量的夹角公式即可得出.
解答:(1)证明:连接AO,设SB=a,则 AO=
a,SO=
a,
又∵SA=
a,∴SO2+OA2=SA2,∴SO⊥OA.
∵SC=SB,∴SO⊥BC.
又∵BC∩OA=O,
∴SO⊥平面ABC.
(2)解:在线段AB上存在一点E是线段AB的中点时,使二面角B-SC-E的平面角的余弦值为
.下面给出证明:
如图以O为原点,以OA,OB,OS所在直线分别为x,y,z轴建系.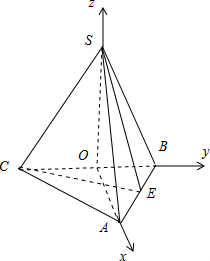
则有O(0,0,0),S(0,0,
a),C(0,-
a,0),B(0,
a,0),A(
a,0,0).
∴
=(-
a,
a,0),
=(0,-
a,-
a).
假设存在E,设
=λ
,则
=
+
=(0,
a,0)+(
aλ,-
,0),
∴
=(
λa,
a-
aλ,0).
设平面SCE的法向量为
=(x,y,z).
由
得
,化为
,令y=-1,则z=1,x=
.
∴
=(
,-1,1).
平面SBC的法向量为
=(1,0,0),∴cos<
,
>=
=
=
,解得λ=
.
∴当E为AB中点时,二面角B-SC-E的平面角的余弦值为
.
| ||
| 2 |
| ||
| 2 |
又∵SA=
| 2 |
∵SC=SB,∴SO⊥BC.
又∵BC∩OA=O,
∴SO⊥平面ABC.
(2)解:在线段AB上存在一点E是线段AB的中点时,使二面角B-SC-E的平面角的余弦值为
| ||
| 5 |
如图以O为原点,以OA,OB,OS所在直线分别为x,y,z轴建系.

则有O(0,0,0),S(0,0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AB |
| ||
| 2 |
| ||
| 2 |
| SC |
| ||
| 2 |
| ||
| 2 |
假设存在E,设
| BE |
| BA |
| CE |
| CB |
| BE |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| CE |
| ||
| 2 |
| 2 |
| ||
| 2 |
设平面SCE的法向量为
| n |
由
|
|
|
| 2-λ | ||
|
∴
| n |
| 2-λ | ||
|
平面SBC的法向量为
| m |
| m |
| n |
| ||||
|
|
| ||||||
|
| ||
| 5 |
| 1 |
| 2 |
∴当E为AB中点时,二面角B-SC-E的平面角的余弦值为
| ||
| 5 |
点评:熟练掌握通过建立空间直角坐标系利用两平面的法向量的夹角公式求二面角的余弦值、及勾股定理的逆定理、等腰三角形的性质、线面垂直的判定定理是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )