题目内容

如图,在棱锥S—ABC中,AB=BC=1,AB⊥BC,SA=SB=SC,E为SB上一点,且SE∶EB=2∶1.

(1)求证:AC⊥SB;

(2)若∠AEC为二面角A-SB-C的平面角,求三棱锥E—ABC的体积.

(1)证明:过S作SO⊥面ABC于O.??

∵SA=SB=SC,?

∴AO=BO=CO.?

∴O为△ABC的重心.?

又∵△ABC中∠ABC=90°,?

∴O为AC中点.∴BO⊥AC.?

∴SB⊥AC.?

(2)解析：若∠AEC为二面角A-SB-C的平面角,则AE⊥SB.?

设EB=k,SE=2k,SA=SB=3k.?

AE2=SA2-SE2=AB2-BE2,?

即9k2-4k2=1-k2k=,SA=.?

AC=,SO==1.?

E到面ABC距离为S到面ABC距离的,∴VE—ABC?=×S△ABC?×SO=××1×1=.

练习册系列答案
相关题目
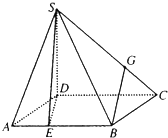精英家教网如图，四棱锥S-ABCD的底面是边长为3的正方形，SD丄底面ABCD，SB=3
3
，点E、G分别在AB，SG 上，且AE=
1
3
AB  CG=
1
3
SC．
（1）证明平面BG∥平面SDE；
（2）求面SAD与面SBC所成二面角的大小．
精英家教网如图，四棱锥S-ABCD的底面是边长为3的正方形，SD丄底面ABCD，SB=3
3
，点E、G分别在AB、SC上，且AE=
1
3
AB，CG=
1
3
SC．
（1）证明：BG∥平面SDE；（2）求面SAD与面SBC所成二面角的大小．
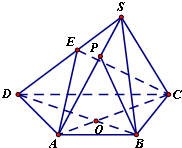如图，四棱锥S-ABCD，底面ABCD是等腰梯形，AB∥DC，tan∠ACB=
1
2
，∠CAB=
π
4
，AC交BD于O．
（1）若SB⊥平面ABCD，求证：面SAC⊥平面SBD；
（2）点E，P分别在SD，SA上，3DE=4ES，AP=2PS，求证：PB∥平面EAC．
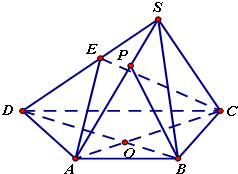如图，四棱锥S-ABCD中，底面ABCD是等腰梯形，AB∥DC，∠CAB=
π
4
，tan∠ACB=
1
2
，AC交BD于O．
（Ⅰ）若SB⊥平面ABCD，求证：AC⊥平面SBD；
（Ⅱ）已知点E，P分别在SD，SA上，满足3DE=4ES，AP=2PS．
求证：PB∥面EAC．
如图，四棱锥S-ABCD中．ABCD为矩形，SD⊥AD，且SD⊥AB，AD=a（a＞0），AB=2AD，SD=
3
AD．E为CD上一点，且CE=3DE．
（1）求证：AE⊥平面SBD；
（2）M、N分别在线段CD、SB上的点，是否存在M、N，使MN⊥CD且MN⊥SB，若存在，确定M、N的位置；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网