题目内容
椭圆
的离心率为
分别是左、右焦点，过F1的直线与圆
相切，且与椭圆E交于A、B两点。
（1）当
时，求椭圆E的方程；
（2）若直线AB的倾斜角为锐角，当c变化时，求证：AB的中点在一定直线上。
解：由椭圆E：
（
）的离心率为
，可设椭圆E：
根据已知设切线AB为：
，
（Ⅰ）圆的圆心
到直线
的距离为
∴切线AB为：
，
联立方程： 
，
∴
，
∴椭圆E的方程为：
。……………………………9分
（Ⅱ）由（Ⅰ）及已知得，AB的中点
，
故弦AB的中点在定直线
（x<0）上。……………………13分
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
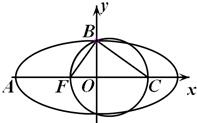如图，F是椭圆
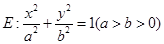的离心率为
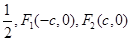分别是左、右焦点，过F1的直线与圆
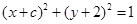相切，且与椭圆E交于A、B两点。
时，求椭圆E的方程；
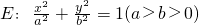的离心率为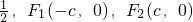
分别是左、右焦点，过F1的直线与圆（x+c）2+（y+2）2=1相切，且与椭圆E交于A、B两点．
时，求椭圆E的方程；
的离心率为
分别是左、右焦点，过F1的直线与圆
相切，且与椭圆E交于A、B两点。
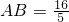时，求椭圆E的方程；