题目内容
椭圆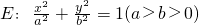 的离心率为
的离心率为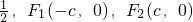 分别是左、右焦点,过F1的直线与圆(x+c)2+(y+2)2=1相切,且与椭圆E交于A、B两点.
分别是左、右焦点,过F1的直线与圆(x+c)2+(y+2)2=1相切,且与椭圆E交于A、B两点.
(1)当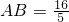 时,求椭圆E的方程;
时,求椭圆E的方程;
(2)若直线AB的倾斜角为锐角,当c变化时,求证:AB的中点在一定直线上.
(1)解:由椭圆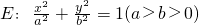 的离心率为
的离心率为 ,可设椭圆E:
,可设椭圆E: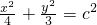
根据已知设切线AB为:y=k(x+c),即kx-y+ck=0,
圆(x+c)2+(y+2)2=1的圆心(-c,-2)到直线kx-y+ck=0的距离为d=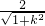 =1
=1
∴k=
∴切线AB为:y= (x+c),与椭圆方程联立,消元可得5x2+8cx=0
(x+c),与椭圆方程联立,消元可得5x2+8cx=0
∴x1=0,x2=- ,
,
∴|AB|= =
= =
=
∴c=1,
∴椭圆E的方程为: .(9分)
.(9分)
(2)证明:由(1)及已知得,AB的中点(-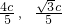 ),
),
故弦AB的中点在定直线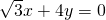 (x<0)上.(13分)
(x<0)上.(13分)
分析:(1)根据椭圆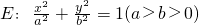 的离心率为
的离心率为 ,可设椭圆E:
,可设椭圆E: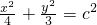 ,设切线AB为:y=k(x+c),即kx-y+ck=0,利用圆(x+c)2+(y+2)2=1的圆心(-c,-2)到直线kx-y+ck=0的距离为d=
,设切线AB为:y=k(x+c),即kx-y+ck=0,利用圆(x+c)2+(y+2)2=1的圆心(-c,-2)到直线kx-y+ck=0的距离为d=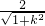 =1,求得斜率,再将直线方程与椭圆方程联立,消元,利用弦长即可求得椭圆E的方程;
=1,求得斜率,再将直线方程与椭圆方程联立,消元,利用弦长即可求得椭圆E的方程;
(2)由(1)及已知得AB的中点(-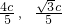 ),从而可得结论.
),从而可得结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,联立方程是关键.
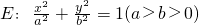 的离心率为
的离心率为 ,可设椭圆E:
,可设椭圆E: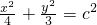
根据已知设切线AB为:y=k(x+c),即kx-y+ck=0,
圆(x+c)2+(y+2)2=1的圆心(-c,-2)到直线kx-y+ck=0的距离为d=
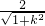 =1
=1∴k=

∴切线AB为:y=
 (x+c),与椭圆方程联立,消元可得5x2+8cx=0
(x+c),与椭圆方程联立,消元可得5x2+8cx=0∴x1=0,x2=-
 ,
,∴|AB|=
 =
= =
=
∴c=1,
∴椭圆E的方程为:
 .(9分)
.(9分)(2)证明:由(1)及已知得,AB的中点(-
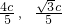 ),
),故弦AB的中点在定直线
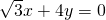 (x<0)上.(13分)
(x<0)上.(13分)分析:(1)根据椭圆
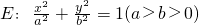 的离心率为
的离心率为 ,可设椭圆E:
,可设椭圆E: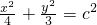 ,设切线AB为:y=k(x+c),即kx-y+ck=0,利用圆(x+c)2+(y+2)2=1的圆心(-c,-2)到直线kx-y+ck=0的距离为d=
,设切线AB为:y=k(x+c),即kx-y+ck=0,利用圆(x+c)2+(y+2)2=1的圆心(-c,-2)到直线kx-y+ck=0的距离为d=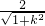 =1,求得斜率,再将直线方程与椭圆方程联立,消元,利用弦长即可求得椭圆E的方程;
=1,求得斜率,再将直线方程与椭圆方程联立,消元,利用弦长即可求得椭圆E的方程;(2)由(1)及已知得AB的中点(-
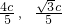 ),从而可得结论.
),从而可得结论.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,联立方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
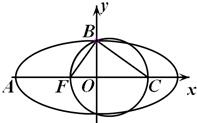 如图,F是椭圆
如图,F是椭圆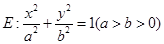 的离心率为
的离心率为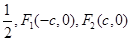 分别是左、右焦点,过F1的直线与圆
分别是左、右焦点,过F1的直线与圆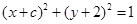 相切,且与椭圆E交于A、B两点。
相切,且与椭圆E交于A、B两点。 时,求椭圆E的方程;
时,求椭圆E的方程;