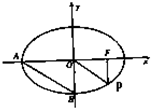
题目内容
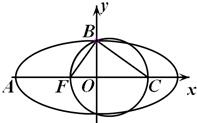 如图,F是椭圆
如图,F是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(1)求椭圆的方程;
(2)过点A的直线l2与圆M交于P,Q两点,且
| MP |
| MQ |
分析:(1)因为椭圆的离心率为
,所以
=
,所以A(-2c,0),B(0,
c),F(-c,0).kBF=
,故kBC=-
,所以BC得方程为y=-
x+
c,由此入手能得到所求的椭圆方程.
(2)因为
•
=|
||
|cos∠PMQ=2×2cos∠PMQ=-2,所以∠PMQ=120°.所以M到直线l2的距离等于1.依题意,直线l2的斜率存在,设直线l2:y=k(x+2),所以
=1,由此能得到所求的直线l2的方程.
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
(2)因为
| MP |
| MQ |
| MP |
| MQ |
| |k+2k| | ||
|
解答:解:(1)因为椭圆的离心率为
,所以
=
,即a=2c,b=
c(2分)
所以A(-2c,0),B(0,
c),F(-c,0).kBF=
,故kBC=-
,
所以BC得方程为y=-
x+
c(4分)
令y=0,得x=3c,即C(3c,0),所以圆M的半径为
FC=2c,圆心M(c,0)
因为圆M恰好与直线l1:x+
y+3=0相切,
所以
=2c,∴c=1,∴a=2,b=
故所求的椭圆方程为
+
=1(8分)
(2)因为
•
=|
||
|cos∠PMQ=2×2cos∠PMQ=-2,
所以∠PMQ=120°.所以M到直线l2的距离等于1(11分)
依题意,直线l2的斜率存在,设直线l2:y=k(x+2),即kx-y+2k=0
所以
=1,解得k=±
,
故所求的直线l2的方程为y=±
(x+2)(15分)
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
| 3 |
所以A(-2c,0),B(0,
| 3 |
| 3 |
| ||
| 3 |
所以BC得方程为y=-
| ||
| 3 |
| 3 |
令y=0,得x=3c,即C(3c,0),所以圆M的半径为
| 1 |
| 2 |
因为圆M恰好与直线l1:x+
| 3 |
所以
| |c+3| |
| 2 |
| 3 |
故所求的椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)因为
| MP |
| MQ |
| MP |
| MQ |
所以∠PMQ=120°.所以M到直线l2的距离等于1(11分)
依题意,直线l2的斜率存在,设直线l2:y=k(x+2),即kx-y+2k=0
所以
| |k+2k| | ||
|
| ||
| 4 |
故所求的直线l2的方程为y=±
| ||
| 4 |
点评:本题考查圆锥曲线的性质和应用,解题时要注意公式的合理运用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
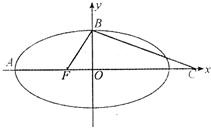 如图,F是椭圆
如图,F是椭圆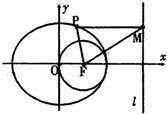 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4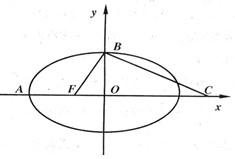 如图,F是椭圆
如图,F是椭圆