题目内容
6.S为△ABC所在平面外-点,SA⊥平面ABC,平面SAB⊥平面SBC,求证:AB⊥BC.分析 作AE⊥SB于E,推导出AE⊥BC,SA⊥BC,由此能证明AB⊥BC.
解答  证明:作AE⊥SB于E,
证明:作AE⊥SB于E,
∵平面SAB⊥平面SBC,∴AE⊥平面SBC,∴AE⊥BC,
又SA⊥平面ABC,∴SA⊥BC,
∴BC⊥平面SAB,
∴AB⊥BC.
点评 本题考查两直线垂直的证明,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
16.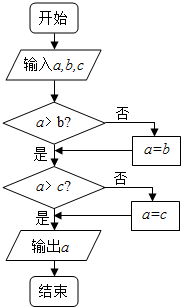 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )
已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )
 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )
已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )| A. | x1 | B. | x2 | C. | x3 | D. | x2或x3 |
14.如果函数f(x)=$\sqrt{x}$在点x=x0处的瞬时变化率是$\frac{\sqrt{3}}{3}$,则x0的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 3 |