题目内容
已知积分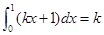 ,则实数
,则实数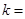 ( )
( )
| A.2 | B.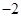 | C.1 | D.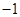 |
A
解析试题分析:
考点:定积分的计算
点评:本题直接套用定积分计算公式: 其中
其中

练习册系列答案
相关题目
定义在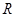 上的可导函数
上的可导函数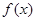 ,当
,当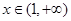 时,
时,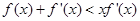 恒成立,
恒成立,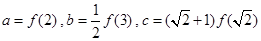 ,则
,则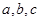 的大小关系为 ( )
的大小关系为 ( )
A.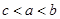 | B.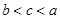 | C.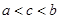 | D. |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( ).
| A.-1<a<2 | B.-3<a<6 |
| C.a<-1或a>2 | D.a<-3或a>6 |
下列函数求导数,正确的个数是 ( )
①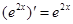 ;②
;②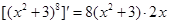 ;③
;③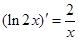 ;④
;④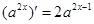
| A.0 | B.1 | C.2 | D.3 |
 在
在 处可导,
处可导, 为常数,则
为常数,则 ( )
( )
A. | B. | C. | D.0 |
设等差数列{an}的前n项和为Sn,已知(a5-1)3+2 011·(a5-1)=1,(a2 007-1)3+2 011(a2 007-1)=-1,则下列结论正确的是( )
| A.S2 011=2 011,a2 007<a5 | B.S2 011=2 011,a2 007>a5 |
| C.S2 011=-2 011,a2 007≤a5 | D.S2 011=-2 011,a2 007≥a5 |
函数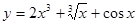 ,则导数
,则导数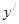 =( )
=( )
A.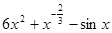 | B. |
C.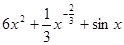 | D. |
已知定义在 上的函数
上的函数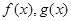 满足
满足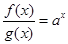 ,且
,且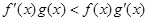 ,
,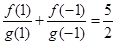 ,若数列
,若数列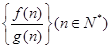 的前
的前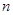 项和等于
项和等于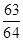 ,则
,则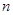 =
=
| A.7 | B.6 | C.5 | D.4 |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
| A.-1<a<2 | B.-3<a<6 | C.a<-1或a>2 | D.a<-3或a>6 |