题目内容
函数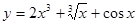 ,则导数
,则导数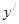 =( )
=( )
A.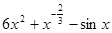 | B. |
C.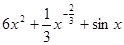 | D. |
D
解析试题分析:根据基本初等函数的导数公式可知, ,因此可知答案为
,因此可知答案为 ,选D.
,选D.
考点:导数的运算
点评:解决的关键是根据导数的基本初等函数的导数公式来求解,属于基础题。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
函数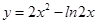 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.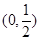 | B.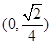 |
C.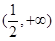 | D.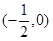 和 和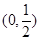 |
设函数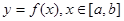 ,其导函数的图象如图所示,则函数
,其导函数的图象如图所示,则函数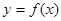 的减区间是
的减区间是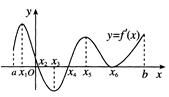
A.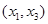 | B.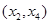 |
C.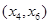 | D.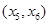 |
已知积分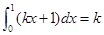 ,则实数
,则实数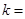 ( )
( )
| A.2 | B.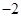 | C.1 | D.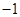 |
曲线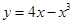 在点(-1,-3)处的切线方程是( )
在点(-1,-3)处的切线方程是( )
A. | B.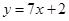 | C. | D.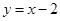 |
函数 的定义域为
的定义域为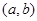 ,其导函数
,其导函数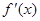 在
在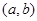 内的图象如图所示,则函数
内的图象如图所示,则函数 在区间
在区间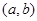 内极大值点的个数是( )
内极大值点的个数是( )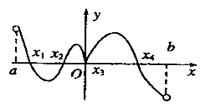
| A.1 | B.2 | C.3 | D.4 |
若 ,则
,则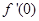 等于 ( )
等于 ( )
| A.-2 | B.-4 | C.2 | D.0 |
已知函数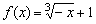 ,则
,则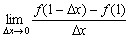 的值为( )
的值为( )
A.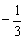 | B.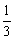 | C.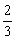 | D.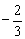 |
设曲线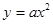 在点(1,
在点(1,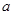 )处的切线与直线
)处的切线与直线 平行,则
平行,则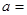 ( )
( )
| A.1 | B.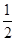 | C.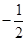 | D.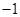 |