题目内容
.圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦。已知点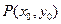 、
、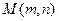 是圆锥曲线C上不与顶点重合的任意两点,
是圆锥曲线C上不与顶点重合的任意两点, 是垂直于
是垂直于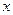 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线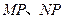 分别交
分别交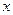 轴于点
轴于点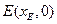 和点
和点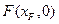 。
。
(1)试用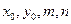 的代数式分别表示
的代数式分别表示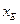
 和
和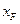 ;
;
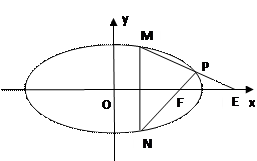
(2)若C的方程为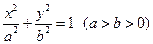 (如图),求证:
(如图),求证: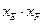 是与
是与 和点
和点 位置无关的定值;
位置无关的定值;
(3)请选定一条除椭圆外的圆锥曲线C,试探究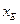 和
和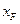 经过某种四则运算(加、减、乘、除),其结果是否是与
经过某种四则运算(加、减、乘、除),其结果是否是与 和点
和点 位置无关的定值,写出你的研究结论并证明。
位置无关的定值,写出你的研究结论并证明。
(说明:对于第3题,将根据研究结论所体现的思维层次,给予两种不同层次的评分)
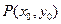 、
、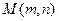 是圆锥曲线C上不与顶点重合的任意两点,
是圆锥曲线C上不与顶点重合的任意两点, 是垂直于
是垂直于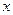 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线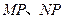 分别交
分别交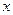 轴于点
轴于点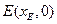 和点
和点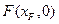 。
。
(1)试用
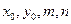 的代数式分别表示
的代数式分别表示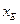
 和
和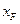 ;
;(2)若C的方程为
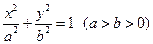 (如图),求证:
(如图),求证: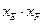 是与
是与 和点
和点 位置无关的定值;
位置无关的定值;(3)请选定一条除椭圆外的圆锥曲线C,试探究
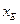 和
和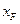 经过某种四则运算(加、减、乘、除),其结果是否是与
经过某种四则运算(加、减、乘、除),其结果是否是与 和点
和点 位置无关的定值,写出你的研究结论并证明。
位置无关的定值,写出你的研究结论并证明。(说明:对于第3题,将根据研究结论所体现的思维层次,给予两种不同层次的评分)
解.(1)因为 是垂直于
是垂直于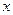 轴的一条垂轴弦,所以
轴的一条垂轴弦,所以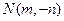
则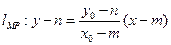 ……………. 2分
……………. 2分
令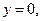 则
则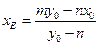 ……………. 4分
……………. 4分
同理可得: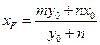 ,……………. 6分
,……………. 6分
(2)由(1)可知: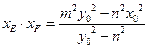 ……………. 8分
……………. 8分
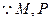 在椭圆C:
在椭圆C: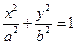 上,
上, ,
,
则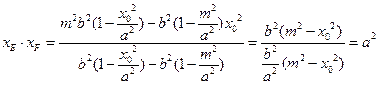 (定值)
(定值)
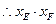 是与
是与 和点
和点 位置无关的定值 …………. 12分
位置无关的定值 …………. 12分
(3)第一层次:
①点 是圆C:
是圆C: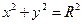 上不与坐标轴重合的任意一点,
上不与坐标轴重合的任意一点, 是垂直于
是垂直于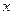 轴的垂轴弦,直线
轴的垂轴弦,直线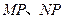 分别交
分别交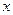 轴于点
轴于点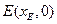 和点
和点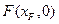 ,则
,则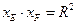 。……………. 16分
。……………. 16分
证明如下:由(1)知: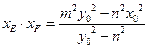
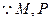 在圆C:
在圆C: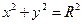 上,
上,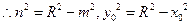 ,
,
则
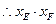 是与
是与 和点
和点 位置无关的定值
位置无关的定值
②点 是双曲线C:
是双曲线C: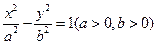 上不与顶点重合的任意一点,
上不与顶点重合的任意一点, 是垂直于
是垂直于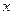 轴的垂轴弦,直线
轴的垂轴弦,直线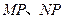 分别交
分别交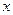 轴于点
轴于点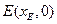 和点
和点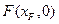 ,
,
则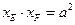 。……………. 16分
。……………. 16分
证明如下:由(1)知: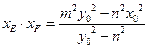
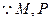 在双曲线C:
在双曲线C: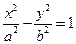 上,
上,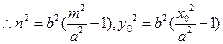 ,
,
则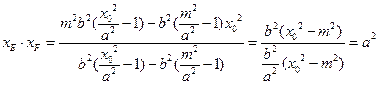
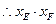 是与
是与 和点
和点 位置无关的定值
位置无关的定值
第二层次:
点 是抛物线C:
是抛物线C: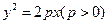 上不与顶点重合的任意一点,
上不与顶点重合的任意一点, 是垂直于
是垂直于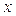 轴的垂轴弦,直线
轴的垂轴弦,直线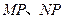 分别交
分别交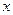 轴于点
轴于点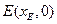 和点
和点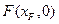 ,则
,则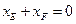 。…………. 18分
。…………. 18分
证明如下:由(1)知: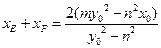 ,
,
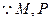 在抛物线C:
在抛物线C: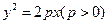 上,
上,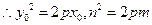
则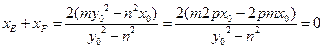
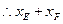 是与
是与 和点
和点 位置无关的定值
位置无关的定值
 是垂直于
是垂直于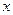 轴的一条垂轴弦,所以
轴的一条垂轴弦,所以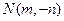
则
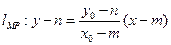 ……………. 2分
……………. 2分令
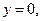 则
则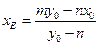 ……………. 4分
……………. 4分同理可得:
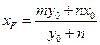 ,……………. 6分
,……………. 6分(2)由(1)可知:
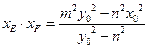 ……………. 8分
……………. 8分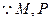 在椭圆C:
在椭圆C: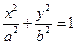 上,
上, ,
,则
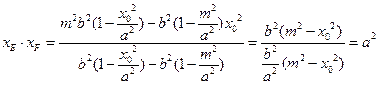 (定值)
(定值)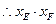 是与
是与 和点
和点 位置无关的定值 …………. 12分
位置无关的定值 …………. 12分(3)第一层次:
①点
 是圆C:
是圆C: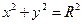 上不与坐标轴重合的任意一点,
上不与坐标轴重合的任意一点, 是垂直于
是垂直于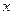 轴的垂轴弦,直线
轴的垂轴弦,直线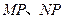 分别交
分别交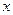 轴于点
轴于点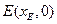 和点
和点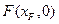 ,则
,则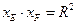 。……………. 16分
。……………. 16分证明如下:由(1)知:
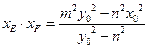
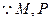 在圆C:
在圆C: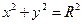 上,
上,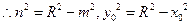 ,
,则

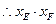 是与
是与 和点
和点 位置无关的定值
位置无关的定值②点
 是双曲线C:
是双曲线C: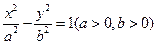 上不与顶点重合的任意一点,
上不与顶点重合的任意一点, 是垂直于
是垂直于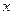 轴的垂轴弦,直线
轴的垂轴弦,直线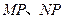 分别交
分别交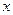 轴于点
轴于点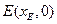 和点
和点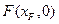 ,
,则
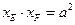 。……………. 16分
。……………. 16分证明如下:由(1)知:
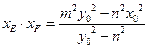
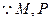 在双曲线C:
在双曲线C: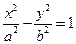 上,
上,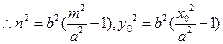 ,
,则
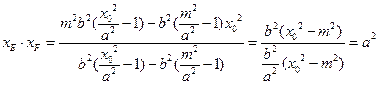
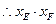 是与
是与 和点
和点 位置无关的定值
位置无关的定值第二层次:
点
 是抛物线C:
是抛物线C: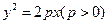 上不与顶点重合的任意一点,
上不与顶点重合的任意一点, 是垂直于
是垂直于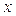 轴的垂轴弦,直线
轴的垂轴弦,直线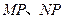 分别交
分别交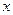 轴于点
轴于点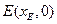 和点
和点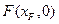 ,则
,则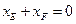 。…………. 18分
。…………. 18分 证明如下:由(1)知:
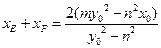 ,
,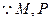 在抛物线C:
在抛物线C: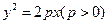 上,
上,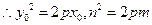
则
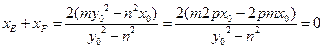
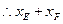 是与
是与 和点
和点 位置无关的定值
位置无关的定值略

练习册系列答案
相关题目
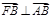 时,其离心率为
时,其离心率为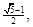 此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( ) 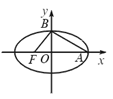
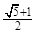
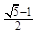
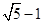
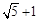
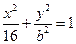
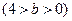 ,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.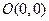 、
、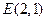 ,试探究是否存在这样的点
,试探究是否存在这样的点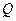 :
: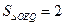 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.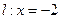 ,
,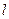 与
与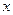 轴交于点
轴交于点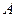 ,动点
,动点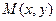 到直线
到直线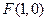 的距离大
的距离大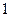 .
.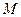 的轨迹
的轨迹
 的方程;
的方程; 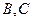 两点,若
两点,若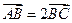 ,求此直线的方程.
,求此直线的方程.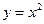 ,
,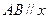 轴.
轴.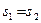 时,求P点的坐标。
时,求P点的坐标。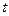 的值,使
的值,使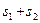 的值最小,并求出最小值。
的值最小,并求出最小值。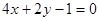 ;②
;② 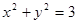 ;③
;③ 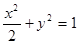 ;④
;④ 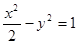 .
.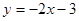 有公共点的所有曲线是 ( )
有公共点的所有曲线是 ( ) 上,则这个正三角形的边长为
上,则这个正三角形的边长为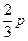
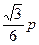
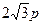
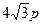
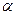 取何值,方程
取何值,方程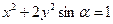 所表示的曲线一定不是( )
所表示的曲线一定不是( )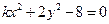 所表示的曲线.
所表示的曲线.