题目内容
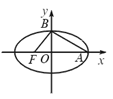
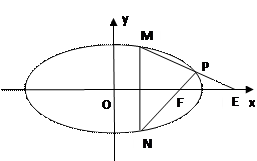
如图,椭圆中心在坐标原点,F为左焦点,当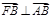 时,其离心率为
时,其离心率为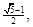 此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
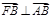 时,其离心率为
时,其离心率为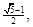 此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( ) 
A.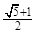 | B.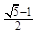 | C.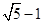 | D.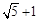 |
A
分析:类比“黄金椭圆”,在黄金双曲线中,当
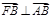 时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.
时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.解:类比“黄金椭圆”,在黄金双曲线中,|OA|=a,|OB|=b,|OF|=c,
当
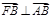 时,|BF|2+|AB|2=|AF|2,
时,|BF|2+|AB|2=|AF|2,∴b2+c2+c2=a2+c2+2ac,
∵b2=c2-a2,整理得c2=a2+ac,
∴e2-e-1=0,解得 e=
 ,或 e=
,或 e= (舍去).
(舍去).故黄金双曲线的离心率e=
 .
.故选A.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目

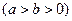 的离心率为
的离心率为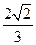 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为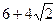 .
.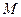 的方程;
的方程;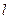 与椭圆
与椭圆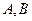 两点,且以
两点,且以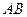 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点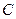 ,
,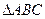 面积的最大值.
面积的最大值. 上有一点
上有一点 ,它到焦点的距离是20,则
,它到焦点的距离是20,则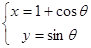 ,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
,直线l:y=2x+b,那么曲C与直线l相切的充要条件是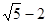
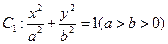 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线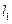 过点
过点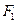 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线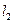 垂直
垂直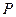 ,线段
,线段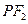 垂直平分线交
垂直平分线交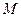
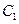 的标准方程和动点
的标准方程和动点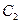 的方程。
的方程。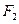 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求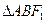 的面积。
的面积。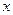 轴交于点
轴交于点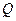 ,不同的两点
,不同的两点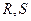 在轨迹
在轨迹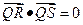 求证:直线
求证:直线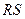 恒过
恒过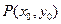 、
、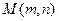 是圆锥曲线C上不与顶点重合的任意两点,
是圆锥曲线C上不与顶点重合的任意两点, 是垂直于
是垂直于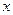 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线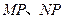 分别交
分别交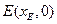 和点
和点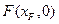 。
。
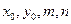 的代数式分别表示
的代数式分别表示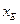
 和
和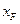 ;
;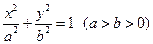 (如图),求证:
(如图),求证: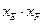 是与
是与 位置无关的定值;
位置无关的定值;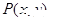 是曲线
是曲线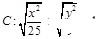 上的点,
上的点,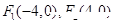 ,则
,则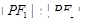 ( )
( )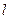 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为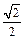 的椭圆C相
的椭圆C相 交于A、B两点,直线y=
交于A、B两点,直线y=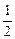 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l 对称,试求直线l与椭圆C的方程
对称,试求直线l与椭圆C的方程