题目内容
3.在△ABC中,D为边BC上的一点,BD=33,$sinB=\frac{5}{13}$,$cos∠ADC=\frac{3}{5}$.求:(1)sin∠BAD;
(2)AD的长.
分析 (1)先求出sin∠ADC=$\frac{4}{5}$,cosB=$\frac{12}{13}$,由sin∠BAD=sin(∠ADC-B),利用正弦加法定理能求出结果.
(2)由正弦定理能求出AD.
解答 解:(1)∵在△ABC中,D为边BC上的一点,cos∠ADC=$\frac{3}{5}$>0,
∴∠ADC<$\frac{π}{2}$,sin∠ADC=$\frac{4}{5}$,
又由已知得B<∠ADC,∴B<$\frac{π}{2}$,
∵$sinB=\frac{5}{13}$,∴cosB=$\frac{12}{13}$,
∴sin∠BAD=sin(∠ADC-B)=sin∠ADCcosB-cos∠ADCsinB
=$\frac{4}{5}×\frac{12}{13}$-$\frac{3}{5}×\frac{5}{13}$
=$\frac{33}{65}$.
(2)由正弦定理得$\frac{AD}{sinB}$=$\frac{BD}{sin∠BAD}$,
∴AD=$\frac{BD•sinB}{sin∠BAD}$=$\frac{33×\frac{5}{12}}{\frac{33}{65}}$=25.
点评 本题考查角的正弦值的求法,考查线段长的求法,是中档题,解题时要认真审题,注意正弦定理和正弦加法定理的合理运用.

练习册系列答案
相关题目
12.将函数$y=2sin(ωx+\frac{π}{3})(ω>0)$的图象分别向左、向右各平移$\frac{π}{3}$个单位后,所得的两个图象的对称轴重合,则ω的最小值为( )
| A. | 3 | B. | $\frac{4}{3}$ | C. | 6 | D. | $\frac{3}{2}$ |
 ,则
,则 为( )
为( )



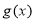 的图象可由函数
的图象可由函数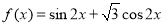 的图象向右平移
的图象向右平移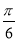 个单位长度变换得到,则
个单位长度变换得到,则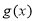 的解析式是( )
的解析式是( )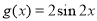
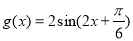

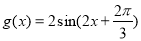
 为
为 上的可导函数,且对
上的可导函数,且对 ,均有
,均有 ,则有( )
,则有( )



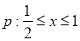 ,命题
,命题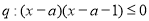 ,若
,若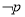 是
是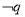 的必要不充分条件,则实数
的必要不充分条件,则实数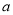 的取值范围是( )
的取值范围是( )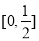 B.
B.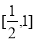
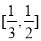 D.
D.