题目内容
已知公差不为0的等差数列 满足
满足 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ) 由等差数列 满足
满足 知,
知, ,所以
,所以 . ①
. ①
因为 成等比数列,所以
成等比数列,所以 ,整理得
,整理得 ,
,
又因为数列 公差不为0,所以
公差不为0,所以 . ② 2分
. ② 2分
联立①②解得 . 4分
. 4分
所以 . 6分
. 6分
(Ⅱ)因为 ,所以
,所以 , 8分
, 8分
所以数列 是以4为首项,8为公比的等比数列, 10分
是以4为首项,8为公比的等比数列, 10分
由等比数列前n项和公式得,  . 12分
. 12分
考点:本题考查等差数列的通项公式,等差数列前n项和公式,等比数列前n项和公式

练习册系列答案
相关题目
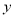 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线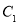 经过点
经过点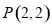 ,以抛物线
,以抛物线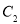 为圆心的圆过定点
为圆心的圆过定点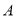 (0,1),记
(0,1),记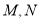 为圆
为圆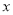 轴的两个交点.
轴的两个交点.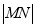 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;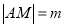 ,
,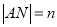 ,求
,求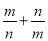 的最大值.
的最大值. ,则图中阴影部分表示的集合为
,则图中阴影部分表示的集合为
 B.
B. C.
C. D.
D.
 是
是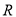 上的奇函数,且在区间
上的奇函数,且在区间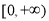 上单调递增,若
上单调递增,若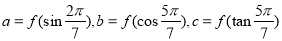 ,则 ( )
,则 ( )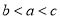 B.
B.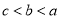 C.
C.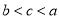 D.
D.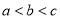
 为圆的内接三角形,
为圆的内接三角形, ,
, 为圆的弦,且
为圆的弦,且 ,过点
,过点 作圆的切线与
作圆的切线与 的延长线交于点
的延长线交于点 ,
, 与
与 交于点
交于点 .
.
 为平行四边形;
为平行四边形; ,
, ,求线段
,求线段 的长.
的长.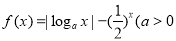 且
且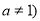 有两个零点
有两个零点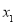 、
、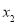 ,则有( )
,则有( )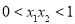 (B)
(B)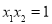 (C)
(C)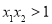 (D)
(D)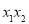 的范围不确定
的范围不确定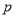 且
且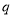 ”为假,则
”为假,则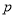 、
、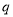 至少有一个是假命题
至少有一个是假命题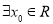 ,
,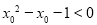 ”的否定是“
”的否定是“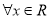 ,
,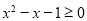 ”
”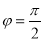 ”是“
”是“ 为偶函数”的充要条件
为偶函数”的充要条件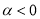 时,幂函数
时,幂函数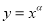 在
在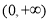 上单调递减
上单调递减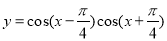 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为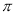 ;
; 且
且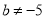 ”是“
”是“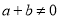 ”的必要不充分条件;
”的必要不充分条件;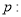 对任意的
对任意的 ,都有
,都有 ,则“
,则“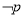 是:存在
是:存在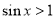 ”;
”;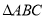 中,若
中,若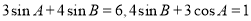 ,则角
,则角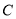 等于
等于 或
或 。
。 ,则△ABC的面积等于 _____.
,则△ABC的面积等于 _____.