题目内容
(12分)已知焦点在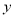 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线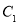 经过点
经过点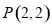 ,以抛物线
,以抛物线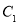 上一点
上一点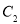 为圆心的圆过定点
为圆心的圆过定点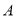 (0,1),记
(0,1),记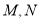 为圆
为圆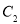 与
与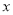 轴的两个交点.
轴的两个交点.
(1)求抛物线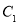 的方程;
的方程;
(2)当圆心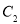 在抛物线上运动时,试判断
在抛物线上运动时,试判断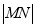 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心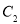 在抛物线上运动时,记
在抛物线上运动时,记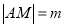 ,
,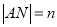 ,求
,求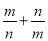 的最大值.
的最大值.
(1) ;(2)是定值(3)
;(2)是定值(3)
【解析】
试题分析:(1)由已知,设抛物线方程为 ,解得p=1.
,解得p=1.
所求抛物线 的方程为
的方程为 .
.
(2)法1:设圆心 ,则圆
,则圆 的半径r=
的半径r=
圆 的方程为
的方程为
令y=0,得 ,得
,得 .
.
 (定值).
(定值).
法2:设圆心 ,因为圆过A(0,1),所以半径r=
,因为圆过A(0,1),所以半径r= ,
,
因为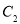 在抛物线上,
在抛物线上, ,且圆被x轴截得的弦长
,且圆被x轴截得的弦长
 (定值)
(定值)
(3)由(2)知,不妨设 ,
,
 ,
,
 ,
,
当a=0时, 时,
时, ,
,
故当且仅当 时,
时, 取得最大值
取得最大值
考点:本题考查抛物线的性质,最值问题,基本不等式的应用.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 ,则“a=±1”是“
,则“a=±1”是“ i为纯虚数”的( )
i为纯虚数”的( ) 的图像向右平移
的图像向右平移 个单位,再向上平移1个单位,所得函数图像对应的解析式为( )
个单位,再向上平移1个单位,所得函数图像对应的解析式为( ) B.
B.
 D.
D.
 ,
, 是双曲线
是双曲线 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点 与点
与点 关于直线
关于直线 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( ) B.
B. C.
C. D.
D.
 中,前n项和为
中,前n项和为 ,已知
,已知 ,则
,则  ( )
( )  B.
B. C.
C. D.
D.
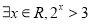 ”的否定是“
”的否定是“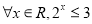 ”;
”;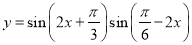 的最小正周期是
的最小正周期是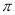 ;
; 在
在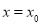 处有极值,则
处有极值,则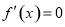 ”的否命题是真命题;
”的否命题是真命题; 上的奇函数,
上的奇函数,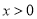 时的解析式是
时的解析式是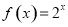 ,
,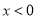 时的解析式为
时的解析式为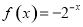 .
. 过点
过点 ,斜率为1,圆
,斜率为1,圆 上恰有1个点到
上恰有1个点到 的值为( ) A.
的值为( ) A. B.
B. C.
C. D.
D.
 在点
在点 处切线与直线
处切线与直线 垂直,则
垂直,则
 满足
满足 ,且
,且 ,
, ,
, 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前 项和为
项和为 .
.