题目内容
已知数列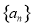 的前n项和为
的前n项和为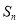 ,
,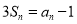
 .
.
(1)求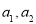 ;
;
(2)求证:数列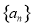 是等比数列;
是等比数列;
(3)求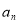 .
.
(1) ,
, (2)(3)见解析
(2)(3)见解析
【解析】
试题分析:(1)由已知 ,可求得数列
,可求得数列 的首项,再由
的首项,再由 递推一个等式即可求得第二项的值.
递推一个等式即可求得第二项的值.
(2)由 ,可求得数列
,可求得数列 的通项,即可得到结论.
的通项,即可得到结论.
(3)由(2)可得结论.
试题解析:(1)【解析】
由 ,得
,得 ,∴
,∴ 。
。
又 ,即
,即 ,得
,得 .
.
(2)证明:当 时,
时, ,得
,得 ,所以
,所以 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(3)【解析】
由(2)可得 .
.
考点:1.数列的递推思想.2.等比数列的性质.
考点分析: 考点1:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的最小值为 ☆
的最小值为 ☆ 
 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.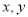 是两个实数,则“
是两个实数,则“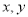 中至少有一个数大于1”是“
中至少有一个数大于1”是“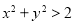 ”成立的( )
”成立的( )
 ,BP=2,求QD.
,BP=2,求QD.
 ,
, .定义:
.定义: ,
, ,……,
,……, ,
, …满足
…满足 的点
的点 称为
称为 的n阶不动点.则
的n阶不动点.则 的n阶不动点的个数是( )
的n阶不动点的个数是( ) 分别与曲线
分别与曲线 ,
, 交于A,B,则
交于A,B,则 的最小值为( )
的最小值为( ) D.
D.
 .
. 的最小正周期;
的最小正周期; 是第一象限角,且
是第一象限角,且 ,求
,求 的值.
的值.