题目内容
17.已知△ABC的三个内角分别为A,B,C,且A≠$\frac{π}{2}$.(Ⅰ)化简$\frac{sin(\frac{3π}{2}+A)•cos(\frac{π}{2}-A)}{cos(B+C)•tan(π+A)}$;
(Ⅱ)若角A满足sinA+cosA=$\frac{1}{5}$.
(i) 试判断△ABC是锐角三角形还是钝角三角形,并说明理由;
(ii) 求tanA的值.
分析 (Ⅰ)由三角形内角和以及诱导公式化简可得原式=cosA;
(Ⅱ)由sinA+cosA=$\frac{1}{5}$和sin2A+cos2A=1,联立可解得sinA=$\frac{4}{5}$,cosA=-$\frac{3}{5}$,可得(i)△ABC是钝角三角形;(ii) tanA=$\frac{sinA}{cosA}$=-$\frac{4}{3}$
解答 解:(Ⅰ)由题意化简可得:
$\frac{sin(\frac{3π}{2}+A)•cos(\frac{π}{2}-A)}{cos(B+C)•tan(π+A)}$
=$\frac{-cosA•sinA}{-cosA•tanA}$=cosA;
(Ⅱ)∵sinA+cosA=$\frac{1}{5}$,又sin2A+cos2A=1,
结合sinA应为正数,联立可解得sinA=$\frac{4}{5}$,cosA=-$\frac{3}{5}$,
∴A为钝角,故可得(i)△ABC是钝角三角形;
(ii) tanA=$\frac{sinA}{cosA}$=-$\frac{4}{3}$
点评 本题考查三角函数恒等变换,涉及三角函数化简求值和同角三角函数基本关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列函数中,值域为[1,+∞)的是( )
| A. | y=2x+1 | B. | y=$\sqrt{x-1}$ | C. | y=$\frac{1}{|x|}$+1 | D. | y=x+$\sqrt{x-1}$ |
12.在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形,现有如图所示两种方案,则( )
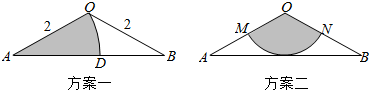

| A. | 方案一中扇形的周长更长 | B. | 方案二中扇形的周长更长 | ||
| C. | 方案一中扇形的面积更大 | D. | 方案二中扇形的面积更大 |
2.已知log0.3(m+1)<log0.3(2m-1),则m的取值范围是( )
| A. | (-∞,2) | B. | $({\frac{1}{2},2})$ | C. | (2,+∞) | D. | (-1,2) |