题目内容
7.若x,y满足条件$\left\{\begin{array}{l}{2x-y≤1}\\{x+y≤2}\\{y-x≤2}\end{array}\right.$,目标函数z=-3x+2y的最小值为-1.分析 作出可行域,变形目标函数,平移直线y=$\frac{3}{2}$x结合图象可得.
解答 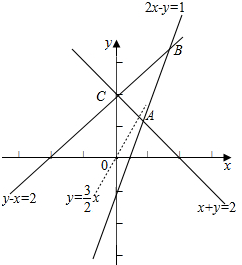 解:作出条件$\left\{\begin{array}{l}{2x-y≤1}\\{x+y≤2}\\{y-x≤2}\end{array}\right.$所对应的可行域(如图△ABC),
解:作出条件$\left\{\begin{array}{l}{2x-y≤1}\\{x+y≤2}\\{y-x≤2}\end{array}\right.$所对应的可行域(如图△ABC),
变形目标函数可得y=$\frac{3}{2}$x+$\frac{1}{2}$z,平移直线y=$\frac{3}{2}$x可知
当直线经过点A时,直线的截距最小,
解方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$可解得A(1,1)
此时目标函数z取最小值z=-3+2=-1
故答案为:-1
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
15.(x+1)2(x-2)4的展开式中含x3项的系数为( )
| A. | 16 | B. | 40 | C. | -40 | D. | 8 |
2.若实数数列:1,a,81成等比数列,则圆锥曲线x2+$\frac{y^2}{a}$=1的离心率是( )
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{3}$或$\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或10 |
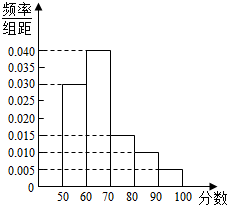 某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.
某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.