题目内容
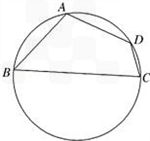
长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界
AB=AD=4万米,BC=6万米,CD=2万米.
(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P;使得棚户区改造的新建筑用地
APCD的面积最大,并求最大值.
AB=AD=4万米,BC=6万米,CD=2万米.
(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P;使得棚户区改造的新建筑用地
APCD的面积最大,并求最大值.
解:(1)因为四边形ABCD内接于圆,
所以∠ABC+∠ADC=180°,连接AC,
由余弦定理:AC2=42+62﹣2×4×6×cos∠ABC=42+22﹣2×2×4cos∠ADC、
所以cos∠ABC= ,
,
∵∠ABC∈(0,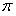 ),
),
故∠ABC=60°.
S四边形ABCD= ×4×6×sin60°+
×4×6×sin60°+ ×2×4×sin120°=8
×2×4×sin120°=8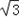 (万平方米).
(万平方米).
在△ABC中,由余弦定理:AC2=AB2+BC2﹣2AB·BCcos∠ABC=16+36﹣2×4×6× .
.
AC=2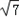 .
.
由正弦定理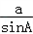 =
=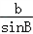 =2R,
=2R,
∴2R=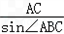 =
=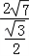 =
=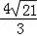 ,
,
∴R=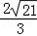 (万米).
(万米).
(2)∵S四边形APCD=S△ADC+S△APC,
又S△ADC= ADCDsin120°=2
ADCDsin120°=2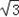 ,
,
设AP=x,CP=y.则S△APC= xysin60°=
xysin60°=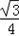 xy.
xy.
又由余弦定理AC2=x2+y2﹣2xycos60°=x2+y2﹣xy=28.
∴x2+y2﹣xy≥2xy﹣xy=xy.
∴xy≤28,当且仅当x=y时取等号
∴S四边形APCD=2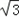 +
+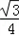 xy≤2
xy≤2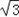 +
+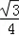 ×28=9
×28=9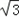 ,
,
∴最大面积为9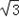 万平方米.
万平方米.
所以∠ABC+∠ADC=180°,连接AC,
由余弦定理:AC2=42+62﹣2×4×6×cos∠ABC=42+22﹣2×2×4cos∠ADC、
所以cos∠ABC=
 ,
,∵∠ABC∈(0,
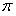 ),
),故∠ABC=60°.
S四边形ABCD=
 ×4×6×sin60°+
×4×6×sin60°+ ×2×4×sin120°=8
×2×4×sin120°=8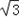 (万平方米).
(万平方米).在△ABC中,由余弦定理:AC2=AB2+BC2﹣2AB·BCcos∠ABC=16+36﹣2×4×6×
 .
.AC=2
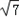 .
.由正弦定理
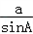 =
=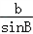 =2R,
=2R,∴2R=
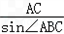 =
=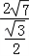 =
=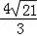 ,
,∴R=
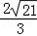 (万米).
(万米).(2)∵S四边形APCD=S△ADC+S△APC,
又S△ADC=
 ADCDsin120°=2
ADCDsin120°=2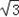 ,
,设AP=x,CP=y.则S△APC=
 xysin60°=
xysin60°=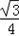 xy.
xy.又由余弦定理AC2=x2+y2﹣2xycos60°=x2+y2﹣xy=28.
∴x2+y2﹣xy≥2xy﹣xy=xy.
∴xy≤28,当且仅当x=y时取等号
∴S四边形APCD=2
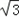 +
+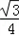 xy≤2
xy≤2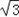 +
+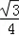 ×28=9
×28=9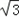 ,
,∴最大面积为9
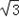 万平方米.
万平方米.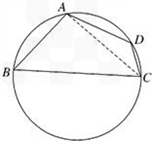

练习册系列答案
相关题目
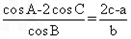 .
.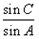 的值;
的值;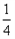 ,b=2, 求△ABC的面积S.
,b=2, 求△ABC的面积S. 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
, 。
。 的面积;
的面积;  ,求
,求 的值。
的值。
 ,求
,求 =
=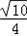 .
.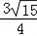 ,且sin2A+sin2B=
,且sin2A+sin2B=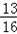 sin2C,求a,b及c的值.
sin2C,求a,b及c的值.