题目内容
已知
（Ⅰ）求函数f（x）的单调增区间．
（Ⅱ）在△ABC中，a、b、c分别是角A、B、C的对边，且a=1，b+c=2，f（A）=
，求
△ABC的面积．
（Ⅰ）求函数f（x）的单调增区间．
（Ⅱ）在△ABC中，a、b、c分别是角A、B、C的对边，且a=1，b+c=2，f（A）=
，求△ABC的面积．
解：（Ⅰ）因为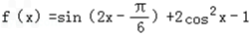
=
=
=
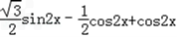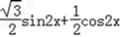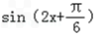
所以函数f（x）的单调递增区间是〔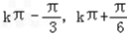
〕（k∈Z）
（Ⅱ）因为f（x）=
，所以
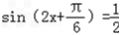
又0＜A＜π所以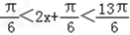
从而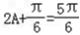
故A=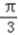
在△ABC中，∵a=1，b+c=2，A=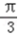
∴1=b2+c2﹣2bccosA，即1=4﹣3bc．
故bc=1从而S△ABC=
=
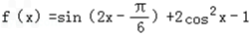
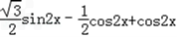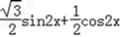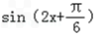
==所以函数f（x）的单调递增区间是〔
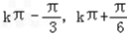〕（k∈Z）（Ⅱ）因为f（x）=
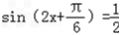
，所以又0＜A＜π所以
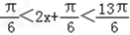
从而
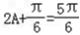故A=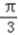在△ABC中，∵a=1，b+c=2，A=
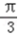
∴1=b2+c2﹣2bccosA，即1=4﹣3bc．
故bc=1从而S△ABC=
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
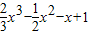，x∈R