题目内容
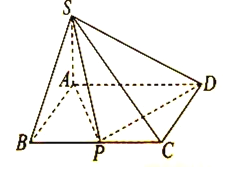
【题目】如图,四棱锥![]() 的底面是矩形,
的底面是矩形,![]() 底面ABCD,P为BC边的中点,SB与平面ABCD所成的角为
底面ABCD,P为BC边的中点,SB与平面ABCD所成的角为![]() ,且
,且![]() ,
,![]() .
.
![]() 1
1![]() 求证:
求证:![]() 平面SAP;
平面SAP;
![]() 2
2![]() 求二面角
求二面角![]() 的余弦的大小.
的余弦的大小.
【答案】(1)见证明;(2)![]()
【解析】
![]() 1
1![]() 欲证
欲证![]() 平面SAP,根据直线与平面垂直的判定定理可知只需证PD与平面SAP内两相交直线垂直,根据题意可知
平面SAP,根据直线与平面垂直的判定定理可知只需证PD与平面SAP内两相交直线垂直,根据题意可知![]() 是SB与平面ABCD所成的角,根据勾股定理可知
是SB与平面ABCD所成的角,根据勾股定理可知![]() ,根据线面垂直的性质可知
,根据线面垂直的性质可知![]() ,而
,而![]() 满足定理所需条件;
满足定理所需条件;
![]() 2
2![]() 设Q为AD的中点,连接PQ,根据
设Q为AD的中点,连接PQ,根据![]() ,
,![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角,在
的平面角,在![]() 中,求出二面角
中,求出二面角![]() 的余弦即可.
的余弦即可.
![]() 1
1![]()
证明:因为![]() 底面ABCD,
底面ABCD,
所以,![]() 是SB与平面ABCD所成的角
是SB与平面ABCD所成的角
由已知![]() ,所以
,所以![]() 易求得,
易求得,![]()
又因为![]() ,所以
,所以![]() ,所以
,所以![]()
因为![]() 底面ABCD,
底面ABCD,![]() 平面ABCD,
平面ABCD,
所以![]() ,
,
由于![]() 所以
所以![]() 平面
平面![]()
![]() 2
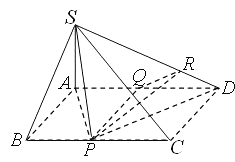
2![]() 设Q为AD的中点,连接PQ,
设Q为AD的中点,连接PQ,
由于![]() 底面ABCD,且
底面ABCD,且![]() 平面SAD,
平面SAD,
则平面![]() 平面
平面![]()
![]() ,
,![]() 平面SAD,
平面SAD,![]() 平面SAD,
平面SAD,![]() .
.
过Q作![]() ,垂足为R,连接PR,则
,垂足为R,连接PR,则![]() 面QPR.
面QPR.
又![]() 面QPR,
面QPR,![]() ,
,![]() 是二面角
是二面角![]() 的平面角
的平面角![]()
容易证明![]() ∽
∽![]() ,则
,则![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]()
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]()
所以二面角![]() 的余弦为
的余弦为![]()

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”


