题目内容
(本小题满分12分)已知函数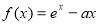 (
(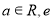 为自然对数的底数).
为自然对数的底数).
(Ⅰ)讨论函数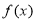 的单调性;
的单调性;
(Ⅱ)若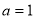 ,函数
,函数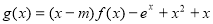 在
在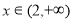 上为增函数,求实数
上为增函数,求实数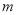 的取值范围.
的取值范围.
(1)当 时,所以
时,所以 在
在 上为增函数,当
上为增函数,当 时,函数
时,函数 在
在 上为减函数,
上为减函数,
所以函数 在
在 上为增函数;(2)
上为增函数;(2) .
.
【解析】
试题分析:(1)函数 在某个区间内可导,则若
在某个区间内可导,则若 ,则
,则 在这个区间内单调递增,若
在这个区间内单调递增,若 ,则
,则 在这个区间内单调递减;(2)若可导函数
在这个区间内单调递减;(2)若可导函数 在指定的区间
在指定的区间 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为
 恒成立,从而构建不等式,要注意“=”是否可以取到;(3)对于恒成立的问题,常用到两个结论:(1)
恒成立,从而构建不等式,要注意“=”是否可以取到;(3)对于恒成立的问题,常用到两个结论:(1) 恒成立
恒成立 ,(2)
,(2) 恒成立
恒成立 ;(4)利用导数方法证明不等式
;(4)利用导数方法证明不等式 在区间
在区间 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数 ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数 ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
试题解析:(Ⅰ)函数 的定义域为
的定义域为

当 时,
时, ,所以
,所以 在
在 上为增函数;
上为增函数;
当 时,由
时,由 得
得
则:当 时,
时, ,所以函数
,所以函数 在
在 上为减函数,
上为减函数,
当 时,
时, ,
,
所以函数 在
在 上为增函数. 6分
上为增函数. 6分
(Ⅱ)当 时,
时, ,
,
∵ 在
在 上为增函数,
上为增函数,

 在
在 恒成立,
恒成立,
即 在
在 恒成立,
恒成立,
令 ,
, ,
,
 ,
,
令 ,
,
 在
在 恒成立,
恒成立,
即 在
在 单调递增,
单调递增,
即 ,
,

即 在
在 单调递增,
单调递增,

所以 . 12分
. 12分
考点:1、利用导数求函数的单调区间;2、函数单调性的应用;3、恒成立的问题.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
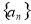 中,
中, 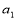 ,
,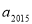 为方程
为方程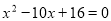 的两根,则
的两根,则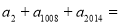 ( )
( ) 内单调递增的函数是( )
内单调递增的函数是( ) B.
B. C.
C.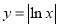 D.
D.
 化为十进制数,结果为 .
化为十进制数,结果为 . ,
, ,
, ,则集合
,则集合 等于( )
等于( ) B.
B. C.
C. D.
D.
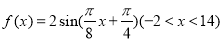 的图象与
的图象与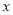 轴交于点
轴交于点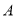 ,过点
,过点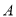 的直线
的直线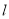 与函数
与函数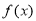 的图象交于
的图象交于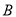 、
、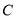 两点,
两点,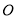 为坐标原点,则
为坐标原点,则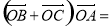 .
. 所表示的平面区域为
所表示的平面区域为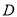 ,若直线
,若直线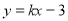 与平面区域
与平面区域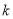 的取值范围为是
的取值范围为是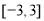

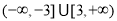

 的首项为
的首项为 ,数列
,数列 为等比数列且
为等比数列且 ,若
,若 ,则
,则 .
. 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系. 的极坐标方程;
的极坐标方程; 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.