题目内容
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
(1)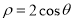 ;(2)2.
;(2)2.
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若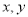 有范围限制,要标出
有范围限制,要标出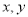 的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式
的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式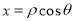 及
及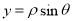 直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如
直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如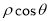 ,
,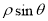 ,
,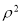 的形式,进行整体代换,其中方程的两边同乘以(或同除以)
的形式,进行整体代换,其中方程的两边同乘以(或同除以)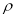 及方程的两边平方是常用的变形方法.
及方程的两边平方是常用的变形方法.
试题解析:圆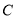 的普通方程为
的普通方程为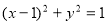 ,又
,又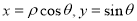
所以圆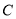 的极坐标方程为
的极坐标方程为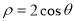 (5分)
(5分)
设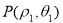 ,则有
,则有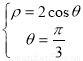 解得
解得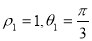
设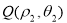 ,则有
,则有 解得
解得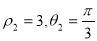
所以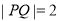 . (10分)
. (10分)
考点:极坐标方程的应用.
考点分析: 考点1:坐标系与参数方程 考点2:参数方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
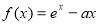 (
(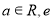 为自然对数的底数).
为自然对数的底数).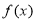 的单调性;
的单调性;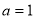 ,函数
,函数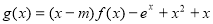 在
在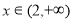 上为增函数,求实数
上为增函数,求实数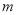 的取值范围.
的取值范围.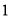 、
、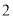 、
、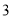 、
、 、
、 中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率为
中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率为 B.
B.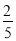 C.
C.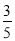 D.
D.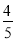
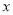 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点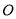 ,并且经过点
,并且经过点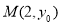 .若点
.若点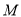 到该抛物线焦点的距离为
到该抛物线焦点的距离为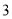 ,则
,则 ( )
( )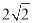 B、
B、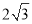 C、
C、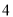 D、
D、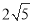
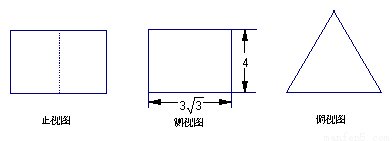
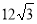 B.
B. C.
C.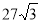 D.
D.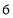
 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率
局时停止.设甲在每局中获胜的概率
 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.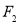 、
、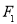 是双曲线
是双曲线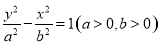 的上、下焦点,点
的上、下焦点,点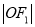 为半径的圆上,则双曲线的离心率为( )
为半径的圆上,则双曲线的离心率为( )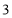 B.
B.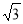 C.
C.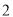 D.
D.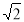
 ,
, ,
, ,
, ,若
,若 ,
, ,则
,则 的最大值是
的最大值是 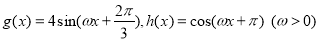 .
. 时,把
时,把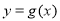 的图像向右平移
的图像向右平移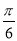 个单位得到函数
个单位得到函数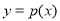 的图像,求函数
的图像,求函数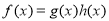 ,若
,若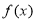 的图象与直线
的图象与直线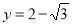 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求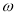 的值,并求函数
的值,并求函数