题目内容
5.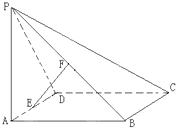 如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,
如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,AP=2AD=4,PD=$2\sqrt{5}$,E为AD的中点,F为PB的中点.
(Ⅰ) 求证:EF‖平面PCD;
(Ⅱ) 当二面角A-PD-B的余弦值为$\frac{1}{4}$时,求AB的长.
分析 (Ⅰ)设G为PC的中点,通过证明EF∥GD,然后证明EF∥平面PCD;
(Ⅱ)以H为坐标原点,以AB所在直线为x轴,HD所在直线为y轴建立空间直角坐标系,求出相关点的坐标,以及平面PAD的法向量,设平面PBD的法向量,通过向量的数量积求解二面角A-PD-B的余弦值为$\frac{1}{4}$时,带带AB的长.
解答 (本题满分14分)
证明(Ⅰ):如图,设G为PC的中点,因为F为PB的中点,所以FG∥BC∥ED,又 E为AD的中点,由已知得:FG=ED=1,所以四边形EFGD为平行四边形.所以EF∥GD,因为EF?平面PCD,GD?平面PCD,所以EF∥平面PCD;
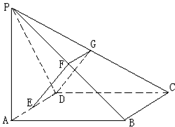
(Ⅱ)解 在△PAD中,AD=2,PA=4,PD=$2\sqrt{5}$,满足PD2=PA2+AD2,所以∠PAD=90°,即PA⊥AD(1),
在底面ABCD中,过点D作DH⊥AB,H为垂足,因为平面PAB⊥ABD,由面面垂直的性质可知:DH⊥平面PAB,
所以DH⊥PA(2),由(1)(2)可得:PA⊥平面ADH,即PA⊥底面ABCD.
以H为坐标原点,以AB所在直线为x轴,HD所在直线为y轴建立空间直角坐标系,
则P(-1,0,4),A(-1,0,0),D(0,$-\sqrt{3}$,0)设B(a,0,0),
这样可得:$\overrightarrow{AP}=(0,0,4)$,$\overrightarrow{PD}=(1,-\sqrt{3},-4)$,$\overrightarrow{DB}=(a,\sqrt{3},0)$,
设平面PAD的法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,则$\left\{{\begin{array}{l}{4{z_1}=0}\\{{x_1}-\sqrt{3}{y_1}-4{z_1}=0}\end{array}}\right.$,取$\overrightarrow{{n}_{1}}=(\sqrt{3},1,0)$,
又设平面PBD的法向量为$\overrightarrow{{n}_{2}}=({x}_{2},{y}_{2},{z}_{2})$,则$\left\{{\begin{array}{l}{a{x_2}+\sqrt{3}{y_2}=0}\\{{x_2}-\sqrt{3}{y_2}-4{z_2}=0}\end{array}}\right.$,取$\overrightarrow{{n}_{2}}=(\sqrt{3},-a,\frac{\sqrt{3}(1+a)}{4})$,
由题设$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{|{3-a}|}}{{2\sqrt{3+{a^2}+\frac{{3{{(1+a)}^2}}}{16}}}}=\frac{1}{4}$,整理得3a2-26a+35=0:
由此可求得$a=\frac{5}{3}$,或a=7(不合题意,舍去)所以AB=$\frac{8}{3}$,
故当二面角A-PD-B的余弦值为$\frac{1}{4}$时,AB的长为$\frac{8}{3}$.
(注:本题也可用几何法解答,过程略)
点评 本题考查直线与平面平行的判定定理的应用,二面角的平面角的求法,空间距离的求法,考查空间想象能力以及计算能力.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{1}}^{2}-n\overline{{x}^{2}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.