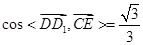题目内容
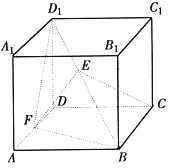
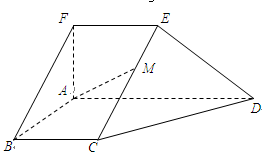
(本题满分12分) 如图,平面 ⊥平面
⊥平面 ,其中
,其中 为矩形,
为矩形, 为梯形,
为梯形, ∥
∥ ,
, ⊥
⊥ ,
, =
= =2
=2 =2,
=2, 为
为 中点.
中点.
(Ⅰ) 证明 ;
;
(Ⅱ) 若二面角 的平面角的余弦值为
的平面角的余弦值为 ,求
,求 的长.
的长.
(Ⅰ) 证明见解析(Ⅱ)
解析试题分析:(Ⅰ)由已知 为正三角形,
为正三角形, 为
为 中点,所以
中点,所以 ,
,
因为平面 ⊥平面
⊥平面 ,平面
,平面
 ⊥平面
⊥平面
 ,
,
所以 平面
平面 ,所以
,所以 . ……4分
. ……4分
(Ⅱ) 方法一:设 .取
.取 的中点
的中点 ,由题意得
,由题意得 .
.
因为平面 ⊥平面
⊥平面 ,
, ,所以
,所以 ⊥平面
⊥平面 ,
,
所以 ,所以
,所以 ⊥平面
⊥平面 .
.
过 作
作 ,垂足为
,垂足为 ,
,
连结 ,则
,则 ,
,
所以 为二面角
为二面角 的平面角. ……8分
的平面角. ……8分
在直角△ 中,
中, ,得
,得 .
.
在直角△ 中,由
中,由 =sin∠AFB=
=sin∠AFB= ,得
,得 =
= ,所以
,所以 =
= .
.
在直角△ 中,
中, ,
, =
= ,得
,得 =
= .
.
因为 =
= =
= ,得x=
,得x= ,所以
,所以 =
= . ……12分
. ……12分
方法二:设 .以
.以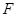 为原点,
为原点, 所在的直线分别为
所在的直线分别为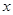 轴,
轴,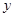 轴建立空间直角坐标系
轴建立空间直角坐标系 .
.
则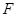 (0,0,0),
(0,0,0),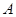 (-2,0,0),
(-2,0,0), (
( ,0,0),
,0,0), (-1,
(-1,

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
 ,
,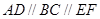 ,
,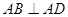 ,
,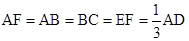
 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由. 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由. 与
与 均为菱形,
均为菱形,  ,且
,且 ,
,
 平面
平面 ;
; 的余弦值。
的余弦值。
 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
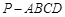 中,
中,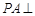 平面
平面 ,
,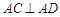 ,
,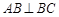 ,
,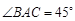 ,
,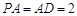 ,
,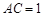 .
.
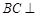 平面
平面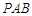
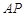 和平面
和平面 所成角的正弦值
所成角的正弦值 的正切值;
的正切值;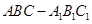 中,
中, ,
,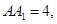 点
点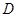 是
是 的中点。
的中点。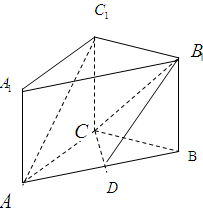

 与平面
与平面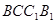 所成的角的正切值
所成的角的正切值