题目内容
已知函数f(x)=ax3+bx2-3x在x=±1处的切线斜率均为0.
(1)求a,b的值;
(2)过点A(0,16)作曲线y=f(x)的切线,求此切线方程.
(1)求a,b的值;
(2)过点A(0,16)作曲线y=f(x)的切线,求此切线方程.
考点:利用导数研究曲线上某点切线方程
专题:综合题,导数的概念及应用
分析:(1)求导数,利用函数f(x)=ax3+bx2-3x在x=±1处的切线斜率均为0,建立方程,即可求a,b的值;
(2)设切点,确定切线方程,代入点A(0,16),即可得出结论.
(2)设切点,确定切线方程,代入点A(0,16),即可得出结论.
解答:
解:(1)∵f(x)=ax3+bx2-3x,
∴f′(x)=3ax2+2bx-3,
∵函数f(x)=ax3+bx2-3x在x=±1处的切线斜率均为0.
∴f′(1)=f′(-1)=0,
∴
,
∴a=1,b=0;
(2)函数f(x)=x3-3x,点A(0,16)不在曲线上,
∵f(x)=x3-3x,∴f′(x)=3x2-3,
设切点为M(a,a3-3a),则f′(a)=3a2-3,
∴切线方程为y-(a3-3a)=(3a2-3)(x-a),
点A(0,16)代入可得16-(a3-3a)=(3a2-3)(-a),
∴a=-2,
∴切点为M(-2,-2),切线方程为9x-y+16=0.
∴f′(x)=3ax2+2bx-3,
∵函数f(x)=ax3+bx2-3x在x=±1处的切线斜率均为0.
∴f′(1)=f′(-1)=0,
∴
|
∴a=1,b=0;
(2)函数f(x)=x3-3x,点A(0,16)不在曲线上,
∵f(x)=x3-3x,∴f′(x)=3x2-3,
设切点为M(a,a3-3a),则f′(a)=3a2-3,
∴切线方程为y-(a3-3a)=(3a2-3)(x-a),
点A(0,16)代入可得16-(a3-3a)=(3a2-3)(-a),
∴a=-2,
∴切点为M(-2,-2),切线方程为9x-y+16=0.
点评:本题考查利用导数研究曲线上某点切线方程,考查学生的计算能力,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
二项式(x2-
)n的展开式中各项系数的和为( )
| 1 |
| x |
| A、32 | B、-32 | C、0 | D、1 |
 已知某种零件使用寿命的频率分布直方图如图,则这种零件的平均使用寿命为
已知某种零件使用寿命的频率分布直方图如图,则这种零件的平均使用寿命为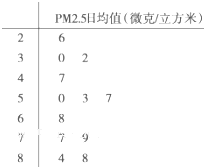 PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶):
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶):