题目内容

19．函数f（x）=x2-2x-4在区间（a，+∞）上是增函数，则a的取值范围为（　　）
A．（-∞，1）B．（-∞，1]C．[1，+∞）D．（1，+∞）

分析 利用二次函数的单调性与对称轴的关系即可得出．

解答 解：∵函数的对称轴为：x=1，函数的单调增区间为：[1，+∞），
函数f（x）=x2-2x-4在区间（a，+∞）上是增函数，
∴a≥1．
故选：C．

点评 熟练掌握二次函数的单调性是解题的关键．

练习册系列答案
相关题目
9．已知函数f（x）=$\sqrt{x+2}+\frac{1}{2x+1}$
（1）求函数f（x）的定义域
（2）求f（-1），当a＞0时，求f（a+1）
（3）判断点$（{2，\frac{11}{5}}）$是否在f（x）的函数图象上．
10．已知函数f（x）定义域是$\{x\left|x\right.≠\frac{t}{2}，t∈Z，x∈R\}$，且f（x）+f（2-x）=0，f（x+1）=-$\frac{1}{f（x）}$，当-1＜x＜-$\frac{1}{2}$时，f（x）=-2-x．
（Ⅰ）证明：f（x）为奇函数；
（Ⅱ）求f（x）在$（\frac{1}{2}，1）$上的表达式；
（Ⅲ）是否存在正整数t，使得$x∈（3t+\frac{1}{2}，3t+1）$时，log2f（x-3t）＞x2-2tx-3t有解，若存在求出t的值，若不存在说明理由．
7．已知命题p：?x∈R，x2+2≥0；写出命题p的否定：?x∈R，x2+2＜0．
14．在等比数列{an}中，an＜0且a1a5+2a42+a3a7=25，则a3+a5=-5．
4．已知$\overrightarrow a=（x，2）$，$\overrightarrow b=（2，-1）$，$\overrightarrow a$∥$\overrightarrow b$，则$|\overrightarrow a+\overrightarrow b|$=（　　）
A．2$\sqrt{5}$B．5C．$\sqrt{10}$D．$\sqrt{5}$
11．下列函数中，既是奇函数又在[0，1]上单调递增的是（　　）
A．y=|x|•x3B．y=xlnxC．y=x•cosxD．$y=-x-\frac{1}{x}$
8．函数f（x）=2x2-2x的单调递增区间是（　　）
A．（-∞，1]B．[1，+∞）C．（-∞，2]D．[2，+∞）
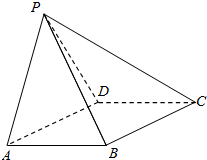9．如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，∠DAB=60°，AB=2，△PAD为等边三角形，平面PAD⊥平面ABCD．
（1）求证AD⊥PB．
（2）在棱AB上是否存在点F，使DF与平面PDC所成角的正弦值为$\frac{2\sqrt{5}}{5}$？若存在，确定线段AF的长度；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网