题目内容
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: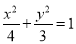 ,直线
,直线 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线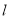 的普通方程;
的普通方程;
(Ⅱ)设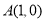 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线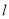 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
(1) ,x-
,x- y+9=0;(2)
y+9=0;(2) .
.
【解析】
试题分析:本题主要考查极坐标方程与直角坐标方程的转化、参数方程与普通方程的转化等基础知识,意在考查考生的分析问题解决问题的能力、转化能力、运算求解能力. 第一问,利用椭圆的参数方程,直接得到将直线的参数方程消参,得到直线的普通方程;第二问,由于P点在椭圆上,结合参数方程设出P点坐标,利用两点间的距离公式,及点到直线的距离公式,再相等,解出 及
及 ,从而得到P点坐标.
,从而得到P点坐标.
试题解析:(Ⅰ)C: (θ为参数),l:x-
(θ为参数),l:x- y+9=0. 4分
y+9=0. 4分
(Ⅱ)设 ,
,
则 ,
,
P到直线l的距离 .
.
由|AP|=d得3sinθ-4cosθ=5,又sin2θ+cos2θ=1,得 ,
, .
.
故 . 10分
. 10分
考点:极坐标方程与直角坐标方程的转化、参数方程与普通方程的转化.
考点分析: 考点1:参数方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)
为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据:
天数t(天) | 3 | 4 | 5 | 6 | 7 |
繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,预测 时,细菌繁殖个数.
时,细菌繁殖个数.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, .
.

 ,其中
,其中 为自然对数的底数.
为自然对数的底数. ,求证:
,求证: ;
; 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值. 在不等式组
在不等式组 表示的平面区域上运动,则
表示的平面区域上运动,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 上有两个动点P,Q,E(3,0)为定点,EP⊥EQ,则
上有两个动点P,Q,E(3,0)为定点,EP⊥EQ,则 最小值为( )
最小值为( ) C. 9 D.
C. 9 D. 
 ,则双曲线的离心率是( )
,则双曲线的离心率是( ) B.
B.  C.
C.  D. 2
D. 2
 的右焦点,过点F向C的一条渐近线引垂直,垂足为A,交另一条渐近线于点B,若
的右焦点,过点F向C的一条渐近线引垂直,垂足为A,交另一条渐近线于点B,若 ,则C的离心率是( )
,则C的离心率是( ) B.
B. C.
C. D. 2
D. 2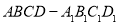 中,底面
中,底面 是正方形,
是正方形,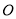 是
是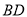 中点,点
中点,点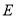 是棱
是棱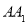 上任意一点.
上任意一点.
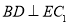 ;
;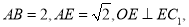 求
求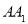 的长
的长