题目内容
(本小题满分12分)在长方体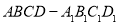 中,底面
中,底面 是正方形,
是正方形,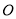 是
是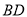 中点,点
中点,点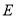 是棱
是棱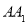 上任意一点.
上任意一点.

(1)证明: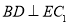 ;
;
(2)若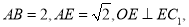 求
求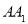 的长
的长
(1)见解析;(2) ;
;
【解析】
试题分析:欲证 ,由于
,由于 只需证明
只需证明 ,下面围绕
,下面围绕 和
和 展开证明即可;
展开证明即可;
第二步借助勾股定理列方程求得即可。
试题解析:(1)证明:连结 ,
, ,由底面是正方形知
,由底面是正方形知 ⊥
⊥
∵ ⊥平面
⊥平面 ,
,
 平面
平面 ∴
∴ ⊥
⊥
由于 ∩
∩ =
= ,所以
,所以 ⊥平面
⊥平面
再由 知
知 ⊥
⊥
(2)设 的长为
的长为 ,连结
,连结 ,
,
在 中,
中, ,
, ,∴
,∴
 中,
中, ,
,
∴
 中,
中,  ,
, ,
,
又∵ ⊥
⊥ ∴
∴
∴4+ +
+ =
= ,∴
,∴
故 的长为
的长为
考点:1.线面平行的判定;2.利用法向量求二面角;
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
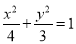 ,直线
,直线 (t为参数).
(t为参数).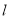 的普通方程;
的普通方程;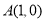 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线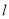 的距离相等,求点P的坐标.
的距离相等,求点P的坐标. ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 的圆心为坐标原点,半径为
的圆心为坐标原点,半径为 ,直线
,直线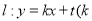 为常数,
为常数,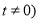 与圆
与圆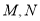 两点,记△
两点,记△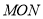 的面积为
的面积为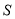 ,则函数
,则函数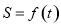 的奇偶性为( )
的奇偶性为( )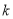 的取值有关
的取值有关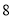 所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )
所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )
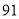 B.
B.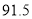 C.
C.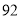 D.
D.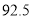
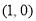 在点
在点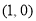 处的切线方程是
处的切线方程是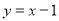 ;
;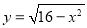 的值域是
的值域是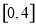 ;
;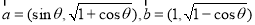 ,其中
,其中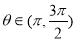 ,则
,则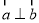 ;
;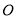 是
是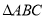 所在平面上一定点,动点P满足:
所在平面上一定点,动点P满足: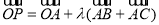 ,
,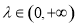 ,则
,则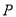 点的轨迹一定通过
点的轨迹一定通过 的重心;
的重心;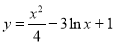 的一条切线的斜率为
的一条切线的斜率为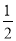 ,则切点的横坐标为( )
,则切点的横坐标为( )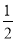
 ,
, ,若
,若 与
与 的夹角为钝角,则实数
的夹角为钝角,则实数 的取值范围是 .
的取值范围是 .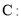
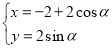 (
(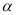 为参数),若以点
为参数),若以点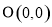 为极点,
为极点,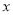 轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .