题目内容
设函数
 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)已知 ,求证:
,求证: ;
;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
(Ⅰ) 见解析;(Ⅱ) 见解析
【解析】
试题分析:(Ⅰ)证明不等式的常用方法,一般还是采用作差或作商,本题采用作差, 


 ;(Ⅱ)由题意
;(Ⅱ)由题意 ,
,
 ,
, (1)当
(1)当 时,∵
时,∵ ,
, ,∴
,∴ 恒成立,即
恒成立,即 ,
, 在
在 上单调递增,所以
上单调递增,所以 .(2)当
.(2)当 时,∵
时,∵ ,
, ,∴
,∴ 恒成立,即
恒成立,即 ,
, 在
在 上单调递减,所以
上单调递减,所以 (3)当
(3)当 时,
时, 得
得 ,
, 在
在 上单调递减,在
上单调递减,在 上单调递增,所以
上单调递增,所以 ,注,本题改编与2014年四川高考题
,注,本题改编与2014年四川高考题
试题解析:(Ⅰ)证明:


 6分
6分
(Ⅱ) ,
,
 ,
,
(1)当 时,∵
时,∵ ,
, ,∴
,∴ 恒成立,
恒成立,
即 ,
, 在
在 上单调递增,
上单调递增,
所以 .
.
(2)当 时,∵
时,∵ ,
, ,∴
,∴ 恒成立,
恒成立,
即 ,
, 在
在 上单调递减,
上单调递减,
所以 .
.
(3)当 时,
时, 得
得
 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以 12分
12分
考点:函数与导数的综合应用
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 关于
关于 平面对称的点
平面对称的点 的坐标为( )
的坐标为( ) B.
B. C.
C. D.
D.
 为假命题,则
为假命题,则 均为假命题;②设
均为假命题;②设 ,命题“若
,命题“若 ,则
,则 ”的否命题是真命题;③直线和抛物线只有一个公共点是直线和抛物线相切的充要条件;则其中正确的个数是( )
”的否命题是真命题;③直线和抛物线只有一个公共点是直线和抛物线相切的充要条件;则其中正确的个数是( ) 的导函数
的导函数 的图像如图所示,那么
的图像如图所示,那么 的图像最有可能的是( )
的图像最有可能的是( )
 ,
, 对应的向量分别是
对应的向量分别是 ,
, ,则复数
,则复数 对应的点位于( )
对应的点位于( )
 绕
绕 轴旋转一周所得的旋转体的体积为 .
轴旋转一周所得的旋转体的体积为 . ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.
 的通项
的通项 ,其前n项和为
,其前n项和为 ,则
,则 为_______.
为_______.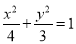 ,直线
,直线 (t为参数).
(t为参数).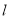 的普通方程;
的普通方程;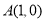 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线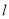 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.