题目内容
19.若不等式a+a(a-1)i<1+ai成立,则实数a为0.分析 利用两个非实数的复数不能够比较大小即可得出.
解答 解:∵不等式a+a(a-1)i<1+ai成立,
∴$\left\{\begin{array}{l}{a<1}\\{a(a-1)=a=0}\end{array}\right.$,
解得a=0.
故答案为:0.
点评 本题考查了两个非实数的复数不能够比较大小的结论,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.命题“对任意实数x,都有x2-2x+1>0”的否定是( )
| A. | 对任意实数x,都有x2-2x+1<0 | B. | 对任意实数x,都有x2-2x+1≤0 | ||
| C. | 存在实数x,有x2-2x+1<0 | D. | 存在实数x,有x2-2x+1≤0 |
10.已知集合A={1,2,3},则“a=3”是“a∈A“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既充分也不必要条件 |
8.已知下列问题:
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.已知α是第二象限角,其终边上一点$P(x,\sqrt{3})$,且$cosα=\frac{{\sqrt{2}}}{4}x$,则sinα=( )
| A. | $-\frac{{\sqrt{6}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
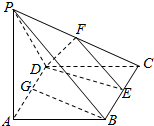 如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,