题目内容
18.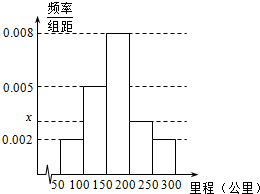 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.(1)求直方图中x的值;
(2)求续驶里程在[200,300]的车辆数;
(3)若从续驶里程在第二组与第五组的车辆中随机抽取2辆车,求两车的续驶里程差大于50公里概率.
分析 (1)利用小矩形的面积和为1,求得x值;
(2)求得续驶里程在[200,300]的车辆的频率,再利用频数=频率×样本容量求车辆数;
(3)利用排列组合,分别求得7辆中随机抽取2辆车的抽法种数与每一组分别抽取一辆车抽法种数,根据古典概型的概率公式计算.
解答 解:(1)由直方图可得:(0.002+0.005+0.008+x+0.002)×50=1,
∴x=0.003;
(2)由题意可知,续驶里程在[200,300]的车辆数为:20×(0.003×50+0.002×50)=5;
(3)由题意可知,续驶里程在第二组[100,150)的车辆数为20×(0.005×50)=5,
续驶里程在第五组[250,300)的车辆数为20×(0.002×50)=2,
从这7辆中随机抽取2辆车,共有C72=21种抽法;
两车的续驶里程差大于50公里,则每一组分别抽取一辆车,共有C51C21=10
∴两车的续驶里程差大于50公里概率P=$\frac{10}{21}$.
点评 本题考查了频率分布直方图,古典概型的概率计算,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
13.已知F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
10.设双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为e,右顶点为A,点Q(3a,0),若C上存在一点P,使得AP⊥PQ,则( )
| A. | $e∈({1,\sqrt{2}})$ | B. | $e∈({\sqrt{2},\sqrt{3}})$ | C. | $e∈({1,\sqrt{3}})$ | D. | $e∈({\sqrt{2},+∞})$ |
7.F1是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点P是双曲线右支上一点,若线段PF1与y轴的交点M恰为PF1的中点,且|OM|=a(O为坐标原点),则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
8.满足{a,b}⊆A?{a,b,c,d,e}的集合A的个数是( )
| A. | 2 | B. | 6 | C. | 7 | D. | 8 |