题目内容
8．偶函数的定义域为R，x∈[0，+∞）时，f（x）=3x+2x2+x．（1）判断f（x）的单调性（不用证明）；
（2）求f（x）在（-∞，0）上的解析式；
（3）解不等式f（a2-3a+7）-f（4a-2a2-5）＞0．
分析 （1）求导数，结合函数是偶函数，判断f（x）的单调性；
（2）设x＜0，则-x＞0，利用条件求f（x）在（-∞，0）上的解析式；
（3）不等式f（a2-3a+7）-f（4a-2a2-5）＞0可化为不等式f（a2-3a+7）＞f（2a2-4a+5），利用函数在[0，+∞）上单调递增，可得a2-3a+7＞2a2-4a+5，即可得出结论．
解答 解：（1）x∈[0，+∞）时，f′（x）=3xln3+4x+1＞0，
∴函数在[0，+∞）上单调递增，
∵函数的偶函数，
∴函数在（-∞，0）上单调递减；
（2）设x＜0，则-x＞0，
∵x∈[0，+∞）时，f（x）=3x+2x2+x，
∴f（-x）=3-x+2x2-x．
∵函数的偶函数，
∴f（x）=3-x+2x2-x；
（3）不等式f（a2-3a+7）-f（4a-2a2-5）＞0可化为不等式f（a2-3a+7）＞f（2a2-4a+5）．
∵函数在[0，+∞）上单调递增，
∴a2-3a+7＞2a2-4a+5，
∴-1＜a＜2．
∴不等式的解集为{a|-1＜a＜2}．
点评 本题考查函数的单调性、奇偶性，考查学生解不等式的能力，确定函数的单调性是关键．
练习册系列答案
字词句段篇系列答案
相关题目
16．设f（x），g（x）在（-∞，+∞）内有定义，f（x）为连续函数，且f（x）≠0，g（x）有间断点，下列函数中必有间断点的为（ ）
| A． | g[f（x）] | B． | [g（x）]2 | C． | f[g（x）] | D． | $\frac{g（x）}{f（x）}$ |
3．f（x）=log${\;}_{\frac{1}{2}}$${\;}^{3{x}^{2}-ax+5}$在[-1，+∞）单调递减，则a的取值范围为（ ）
| A． | （-∞，-6] | B． | （-8，-6] | C． | （-8，-6） | D． | [-6，+∞） |
13．已知函数f（x）=lg（x+1）-ln（1-x）的定义域为A，g（x）=$\sqrt{2x-1}$的定义域为B，则A∩B=（ ）
| A． | （-∞，1） | B． | （-1，$\frac{1}{2}$] | C． | [$\frac{1}{2}$，1） | D． | （1，+∞） |
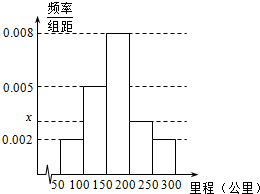某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．