题目内容
13.已知F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2,则双曲线C的离心率为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 设|BF1|=m,则|AF2|=2m,由双曲线的定义可得|AF1|=2a+2m,|BF2|=m+2a,|EF2|=m+2a-2,再由内切圆的性质,求得a=1,结合离心率公式,可得所求.
解答 解:设|BF1|=m,则|AF2|=2m,
即有|AF1|=2a+2m,
|BF2|=m+2a,|EF2|=m+2a-2,
即有2a+2m=2m-(m+2a-2)+2+m,
解得a=1,
由c=2,可得e=$\frac{c}{a}$=2.
故选:D.
点评 本题考查双曲线的定义、方程和性质,考查内切圆的性质,考查离心率的求法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.f(x)=log${\;}_{\frac{1}{2}}$${\;}^{3{x}^{2}-ax+5}$在[-1,+∞)单调递减,则a的取值范围为( )
| A. | (-∞,-6] | B. | (-8,-6] | C. | (-8,-6) | D. | [-6,+∞) |
4.抛物线y=ax2与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x1,x2,直线与x轴交点的横坐标是x3,则恒有( )
| A. | x3=x1+x2 | B. | x1x2=x1x3+x2x3 | ||
| C. | x1+x2+x3=0 | D. | x1x2+x2x3+x3x1=0 |
1.动圆M经过点A(3,0)且与直线l:x=-3相切,则动圆圆心M的轨迹方程是( )
| A. | y2=12x | B. | y2=6x | C. | y2=3x | D. | y2=24x |
8.已知动点A在圆x2+y2=1上移动,点B(3,0),则AB的中点的轨迹方程是( )
| A. | (x+3)2+y2=4 | B. | (x-3)2+y2=1 | C. | (2x-3)2+4y2=1 | D. | (x+$\frac{3}{2}$)2+y2=$\frac{1}{2}$ |
5.在△ABC中,“sinA>sinB”是“a>b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.直线xsinα+y+2=0的倾斜角的取值范围是( )
| A. | [0,π) | B. | [0,$\frac{π}{4}$]∪[$\frac{3}{4}$π,π) | C. | [0,$\frac{π}{4}$] | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,π) |
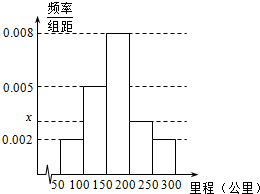 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图. 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.