题目内容
在空间直角坐标系O-xyz中有8个点:P1(1,1,1)、P2(-1,1,1)、…、P7(-1,-1,-1)、P8(1,-1,-1)(每个点的横、纵、竖坐标都是1或-1),以其中4个点为顶点的三棱锥一共有________个(用数字作答).
58
[解析] 这8个点构成正方体的8个顶点,此题即转化成以正方体的8个顶点中的4个点为顶点的三棱锥一共有多少个.从正方体的8个顶点中任取4个,有不同取法C 种,其中这四点共面的(6个对角面、6个表面)共12个,∴这样的三棱锥有C
种,其中这四点共面的(6个对角面、6个表面)共12个,∴这样的三棱锥有C -12=58个.
-12=58个.

练习册系列答案
相关题目
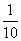 B.
B.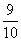
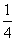 D.
D.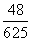
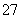 A
A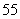 B.C
B.C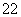
 D.C
D.C
 (sinx+cosx)dx,则二项式(a
(sinx+cosx)dx,则二项式(a +
+ )8展开式中含x项的系数是________.
)8展开式中含x项的系数是________.