题目内容
甲和乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
A.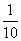 B.
B.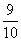
C.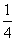 D.
D.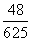
B
[解析] 当甲乙二人在同一岗位时,采用捆绑法将甲乙看作一人,此时的分配方案有A 种,五人任意分配到四个岗位有C
种,五人任意分配到四个岗位有C A
A 种,所以甲乙在一起的概率为
种,所以甲乙在一起的概率为 =
=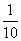 ,甲乙不在一起的概率为1-
,甲乙不在一起的概率为1-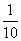 =
=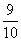 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x,y的取值如下表:
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
从所得的散点图分析可知:y与x线性相关,且 =0.95x+a,则a=( )
=0.95x+a,则a=( )
A.1.30 B.1.45
C.1.65 D.1.80
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |

(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程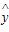 =bx+a,并在坐标系中画出回归直线;
=bx+a,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注:b= ,a=
,a= -b
-b )
)
 B.
B. D.
D.

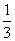 D.
D.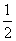
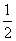 B.
B.
 D.
D.