题目内容
【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
【答案】
(1)解:∵ ![]() ,由正弦定理可得sinCsinA=
,由正弦定理可得sinCsinA= ![]() sinAcosC,
sinAcosC,
sinA≠0,
∴ ![]() ,
,
得 ![]() ,
,
∵C∈(0,π),
∴ ![]() .
.
(2)解:∵sinC+sin(B﹣A)=5sin2A,sinC=sin(A+B),
∴sin(A+B)+sin(B﹣A)=5sin2A,
∴2sinBcosA=2×5sinAcosA,
∵△ABC为斜三角形,
∴cosA≠0,
∴sinB=5sinA,
由正弦定理可知b=5a (1)
由余弦定理c2=a2+b2﹣2abcosC,
∴ ![]() ,(2)
,(2)
由(1)(2)解得a=5,b=1,
∴ ![]()
【解析】(1)由 ![]() ,利用正弦定理可得sinCsinA=
,利用正弦定理可得sinCsinA= ![]() sinAcosC,于是
sinAcosC,于是 ![]() ,即可得出;(2)由sinC+sin(B﹣A)=5sin2A,sinC=sin(A+B),可得sinB=5sinA,由正弦定理可知b=5a,由余弦定理c2=a2+b2﹣2abcosC,联立解出,再利用三角形面积计算公式即可得出.
,即可得出;(2)由sinC+sin(B﹣A)=5sin2A,sinC=sin(A+B),可得sinB=5sinA,由正弦定理可知b=5a,由余弦定理c2=a2+b2﹣2abcosC,联立解出,再利用三角形面积计算公式即可得出.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式: 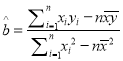 ,
, ![]() .
.