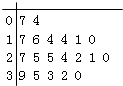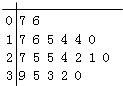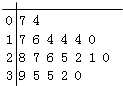题目内容
【题目】国内某知名连锁店分店开张营业期间，在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该分店经理对开业前
天参加抽奖活动的人数进行统计， 
表示开业第
天参加抽奖活动的人数，得到统计表格如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析，发现
与
具有线性相关关系.
（1）若从这
天中随机抽取两天，求至少有
天参加抽奖人数超过
的概率；
（2）请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
，并估计若该活动持续
天，共有多少名顾客参加抽奖.
参考公式：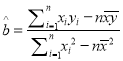 
， 
.
【答案】（1）
（2）140
【解析】试题分析：（1）先根据枚举法确定
天中随机抽取两天总事件数为21种，从中挑出至少有1天参加抽奖人教超过
的事件数
种，最后根据古典概型概率公式求概率，（2）由公式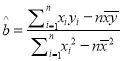
，可得
，再求均值
，并由
可得
，进而可得线性回归方程
；再根据线性回归方程预测第8,9,10天人数，相加得到10天总人数.
试题解析：（1）这
天中参加抽奖的人数没有超过
的为第
天,超过
的为第
天.从这
天中
任取两天的情况有
,
，共
种.其中至少有1天参加抽奖人教超过
的有
种，所以
.
（2）依题意： 
，
，
，
， 
，
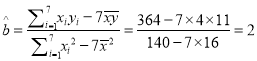则
关于
的线性回归方程为
.
预测
时， 
， 
时， 
， 
时， 
，
则此次活动参加抽奖的人数约为
人.
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
【题目】某学校为倡导全体学生为特困学生捐款，举行“一元钱，一片心，诚信用水”活动，学生在购水处每领取一瓶矿泉水，便自觉向捐款箱中至少投入一元钱．现统计了连续5天的售出和收益情况，如表：
售出水量x（单位：箱） | 7 | 6 | 6 | 5 | 6 |
收益y（单位：元） | 165 | 142 | 148 | 125 | 150 |
（1）求y关于x的线性回归方程；
（2）预测售出8箱水的收益是多少元？
附：回归直线的斜率和截距的最小二乘法估计公式分别为： 
= 
， 
= 
﹣ 
，
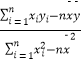参考数据：7×165+6×142+6×148+5×125+6×150=4420．
