题目内容
【题目】甲、乙、丙、丁和戊5名学生进行某种劳动技术比赛，决出了第1到第5名的名次.甲乙两名参赛者去询问成绩，回答者对甲说，“很遗憾，你和乙都没没有拿到冠军.”对乙说，“你当然不会是最差的.”从这个回答分析，甲是第五名的概率是______.
【答案】
【解析】
甲、乙不是第一名且乙不是最后一名，乙的限制多，故先排乙，有
种情况；再排甲，也有种情况；余下的问题是三个元素在三个位置全排列，根据分步计数原理得到结果，再求出甲是第五名包含的不同情况的种数，求出结果.
解：由题意可知，甲、乙不是第一名且乙不是最后一名，
乙的限制多，故先排乙，有种情况，即第二、三、四名；
再排甲，也有种情况，余下人有
种排法.
故共有
种不同的情况，
其中甲是第五名包含的不同情况有：
先排乙，有种情况，即第二、三、四名，甲是第五名，余下人有种排法，
故甲是第五名包含的不同情况有
，
所以甲是第五名的概率为
.
故答案为：.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某互联网公司为了确定下一季度的前期广告投入计划，收集了近
个月广告投入量
（单位：万元）和收益
（单位：万元）的数据如下表：
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①
，②
分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：
|
|
|
|
|
|
|
|
（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；
（Ⅱ）残差绝对值大于
的数据被认为是异常数据，需要剔除：
（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程
（ⅱ）若广告投入量
时，该模型收益的预报值是多少？
附：对于一组数据
，
，……，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
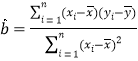
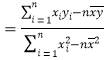【题目】微信已成为人们常用的社交软件，“微信运动”是由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数，同时也可以和好友进行运动量的PK或点赞.现从小明的微信朋友圈内随机选取了50人（男、女各25人），并记录了他们某一天的走路步数，并将数据整理如下表：
步数 性别 | 0~3000 | 3001~6000 | 6001~9000 | 9001~12000 | >12000 |
男 | 1 | 1 | 3 | 15 | 5 |
女 | 0 | 4 | 11 | 8 | 2 |
若某人一天走路的步数超过9000步被系统评定为“积极型”，否则被系统评定为“懈怠型”。
（1）利用样本估计总体的思想，估计小明的所有微信好友中每日走路步数超过12000步的概率；
（2）根据题意完成下面的2×2列联表，并据此判断能否有99.5%的把握认为“评定类型”与“性别”有关？
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附：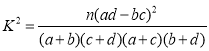
，其中
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
