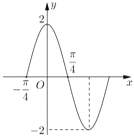
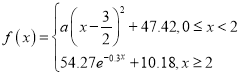题目内容
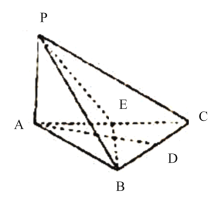
【题目】如图(1)所示,五边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() 的中点,且
的中点,且![]() ,现沿
,现沿![]() 翻折,使得
翻折,使得![]() ,得到的图形如图(2)所示.
,得到的图形如图(2)所示.
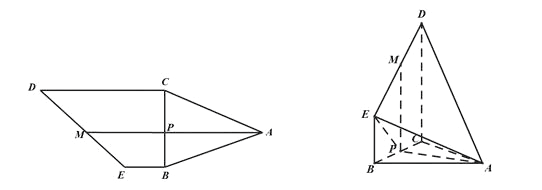
图(1) 图(2)
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成角的平面角的余弦值为
所成角的平面角的余弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析(2)![]()
【解析】
试题(1)根据二面角定义得![]() 是二面角
是二面角![]() 的平面角,即得平面
的平面角,即得平面![]() 平面
平面![]() .由等腰三角形性质得
.由等腰三角形性质得![]() ,根据面面垂直性质定理得
,根据面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() .根据勾股定理得
.根据勾股定理得![]() ,最后根据线面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解得平面
,最后根据线面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解得平面![]() 一个法向量,根据向量数量积求夹角,最后根据线面角与向量夹角互余关系列方程,解得
一个法向量,根据向量数量积求夹角,最后根据线面角与向量夹角互余关系列方程,解得![]() 的值.
的值.
试题解析:(1)如图,连接![]() .因为
.因为![]() ,且
,且![]() 是二面角
是二面角![]() 的平面角,故平面
的平面角,故平面![]() 平面
平面![]() .
.
因为![]() ,
,![]() 为线段
为线段![]() 的中点,故
的中点,故![]() ,
,
因为平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,故
,故![]() .
.
,故![]() ,
,
即![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() .
.

(2)因为![]() ,所以
,所以![]() ,由(I)知,
,由(I)知,![]() 平面
平面![]() ,所以
,所以![]() 两两垂直,
两两垂直,
如图,建立空间直角坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,
,
由 得
得![]() 令
令![]() 可得
可得![]() ,故
,故![]() ;
;
又![]() 为平面
为平面![]() 的一个法向量,平面
的一个法向量,平面![]() 与平面
与平面![]() 所成角的平面角的余弦值为
所成角的平面角的余弦值为![]() ,
,
所以 ,解得
,解得![]() (负值舍去),故
(负值舍去),故![]() .
.

【题目】某企业为提高生产质量,引入了一批新的生产设备,为了解生产情况,随机抽取了新、旧设备生产的共200件产品进行质量检测,统计得到产品的质量指标值如下表及图(所有产品质量指标值均位于区间![]() 内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
质量指标 | 频数 |
| 2 |
| 8 |
| 10 |
| 30 |
| 20 |
| 10 |
合计 | 80 |
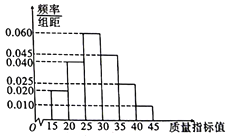
(1)根据上述图表完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为产品质量高与引人新设备有关;
的把握认为产品质量高与引人新设备有关;
新旧设备产品质量![]() 列联表
列联表
产品质量高 | 产品质量一般 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
(2)从旧设备生产的质量指标值位于区间![]() 的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于
的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于![]() 的概率.
的概率.
附: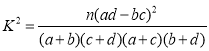 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |